题目描述

Prof. Du and Prof. Pang plan to build a sky garden near the city of Allin. In the garden, there will be a plant maze consisting of straight and circular roads.

On the blueprint of the plant maze, Prof. Du draws $n$ circles indicating the circular roads. All of them have center $(0, 0)$. The radius of the $i$-th circle is $i$.

Meanwhile, Prof. Pang draws $m$ lines on the blueprint indicating the straight roads. All of the lines pass through $(0, 0)$. Each circle is divided into $2m$ parts with equal lengths by these lines.

Let $Q$ be the set of the $n+m$ roads. Let $P$ be the set of all intersections of two different roads in $Q$. Note that each circular road and each straight road have two intersections.

For two different points $a\in P$ and $b\in P$, we define $dis(\{a, b\})$ to be the shortest distance one needs to walk from $a$ to $b$ along the roads. Please calculate the sum of $dis(\{a, b\})$ for all $\{a, b\}\subseteq P$.

输入格式

The only line contains two integers $n,m~(1\le n,m\le 500)$.

输出格式

Output one number -- the sum of the distances between every pair of points in $P$.

Your answer is considered correct if its absolute or relative error does not exceed $10^{-6}$.

1 2

14.2831853072

2 3

175.4159265359

提示

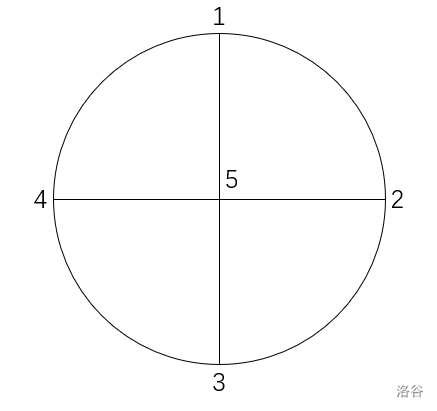
$dis(p_1, p_2)=dis(p_2, p_3)=dis(p_3, p_4)=dis(p_1, p_4)=\frac{\pi}{2}$

$dis(p_1, p_5)=dis(p_2, p_5)=dis(p_3, p_5)=dis(p_4, p_5)=1$

$dis(p_1, p_3)=dis(p_2, p_4)=2$