题目背景

Bessie 带着他的奶牛姐妹们来跳舞了。

她们已经规划好了跳舞的步骤，但是为了更加美观，她们需要知道其中一些头奶牛在某时的平均位置，已达到更完美的表演效果。

不幸的是，由于 Bessie 的姐妹太多了，最多会有 $8\times 10^4$ 只奶牛同时来跳舞。她没有什么方便且快速的方法算这些平均位置，所以向你求助。

题目描述

Bessie 和她的姐妹们已经排好了位置，第 $i$ 头奶牛的坐标为 $(x_i,y_i)$。其中，$x_i$ 是 $x$ 轴坐标，$y_i$ 是 $y$ 轴坐标。

她们的舞蹈队形会有这几种变换方式：

1. 移动：$x$ 到 $y$ 号奶牛的 $x_i\to x_i+a$，$y_i\to y_i+b$。
2. 旋转：$x$ 到 $y$ 号奶牛以 $(a,b)$ 为旋转中心顺时针旋转 $g°$。
3. 散开: $x$ 到 $y$ 号奶牛以 $(a,b)$ 为中心散开为 $\dfrac{p}{q}$ 倍。即设之前奶牛坐标为 $A$，散开后坐标为 $B$，$(a,b)$ 为 $G$，$\overrightarrow{GB}=\dfrac{p}{q}\overrightarrow{GA}$。

Bessie 想知道：对于 $x$ 到 $y$ 号奶牛，他们的平均位置 $(\frac{\sum\limits^y_{i=x}x_i}{y-x+1},\frac{\sum\limits^y_{i=x}y_i}{y-x+1})$。

舞会就要开始了，所以她只能给你 $\texttt{1s}$ 的时间。

输入格式

第一行两个整数，$n,m$。

接下来 $n$ 行，每行两个整数 $x_i,y_i$，表示第 $i(1\le i\le n)$ 个点的坐标

接下来 $m$ 行，每行第一个整数为 $opt$。

若 $opt=1$，则接下来包含四个整数 $x,y,a,b$，进行一次移动操作。

若 $opt=2$，则接下来包含五个整数 $x,y,a,b,g$，进行一次旋转操作。

若 $opt=3$，则接下来包含六个整数 $x,y,a,b,p,q$，进行一次散开操作。

若 $opt=4$，则接下来包含两个整数 $x,y$，表示询问编号为 $x \sim y$ 的奶牛的平均位置。

输出格式

即询问结果，以换行隔开，答案误差允许在 $10^{-4}$ 的范围内。

3 7
1 1
1 3
3 1
1 1 2 1 -2
4 1 3
2 1 3 2 0 270
4 1 2
3 1 2 2 2 2 1
4 1 3
4 3 3

2.3333333333 0.3333333333
2.0000000000 0.0000000000
1.6666666667 -1.0000000000
1.0000000000 1.0000000000

提示

【样例解释】

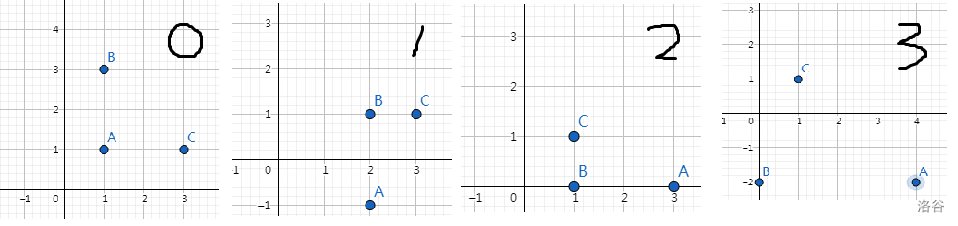
$0$ 为初始情况。$1$ 为进行样例中 1 1 2 1 -2 操作后结果。$2$ 为进行样例中 2 1 3 2 0 270 操作后结果。$3$ 为进行样例中 3 1 2 2 2 2 1 操作后结果。

【数据范围与约定】

保证运算时所有数的绝对值小于或等于 $10^{15}$。

对于 $100\%$ 的数据，$1\le n,m\le3\times10^5$，$1\le x\le y\le n$，$-32768\le a,b<32768$，$0< \dfrac{p}{q}\le 233333$，$0\le g\le359$，初始坐标限制同 $a,b$。

注：

• 请注意常数因子优化。
• 此题输入输出量较大，建议使用 scanf 和 printf。