题目背景

村纱水密是控制着圣辇船的船长。因为是一生和船相伴的船幽灵，因此对船只非常感兴趣。正因为这样的爱好，村纱有一大堆船模。

由于间歇泉的喷发，间歇泉的周围出现了一个汇聚了多方水流的大水坑。不同的水流交错，形成了大大小小的水道。只需要把船模放在某个位置，它就会顺着水流流动。根据物理原理，船自然会从高处流向低处。由于水坑由四处的水汇集而成，因此水坑的中央地势最低；随着到中央距离的增加，地势不断增加。

村纱发现，当她选定了两个位置放下船模后，它们会在某个水流的交汇处发生碰撞。村纱关心碰撞发生的位置。容易发现，第一个可能会产生碰撞的位置，就是在树形结构上这两个选定的点的最近公共祖先。

当然了，由于间歇泉并不稳定，因此水池中央的位置可能会不断变化，地势也不断变化，但是水道并不会发生任何改变。村纱给每个交汇处标上了一个数值「危险程度」，表示两个船模在此处碰撞可能会发生的危险的大小。村纱放置船模的位置也是随机的。

不过由于水坑实在是太大，水坑中央又不断变化，因此只关心船模的村纱被绕晕了。她迫切地想知道在水坑处玩船模产生的威胁，因此希望你帮她计算。

题目描述

这些水道形成了一棵以 $1$ 为根的节点数为 $n$ 的树形结构 $T$。每个节点上有一个点权 $w_i$，表示它的危险程度。现做出如下定义：

• 最近公共祖先：在一棵以 $r$ 为根的有根树上，两个节点 $u,v$ 的最近公共祖先，就是这两个点的公共祖先里面，离根最远的那个，记作 $\operatorname{lca}(r,u,v)$。
• 子树：树 $T$ 上，删掉节点 $u$ 与父亲相连的边后，该结点所在的子图记为子树 $T_u$。特别地，$T$ 本身可以认为是以 $1$ 为根节点的子树 $T_1$。
• 危险值：对于 $T_u$ 而言，它的危险值被定义为：

现在给出 $T$，希望你对于 $i=1,2,\cdots n$，求出 $\mathrm{LCAS}(i)$。

输入格式

• 第一行有一个正整数 $n$，表示节点的个数。
• 第二行有 $n$ 个整数 $w_i$，表示每个结点的危险程度。
• 接下来 $n-1$ 行，每行有两个正整数 $u,v$，描述 $T$ 中的一条边。

输出格式

• 共 $n$ 行 $n$ 个整数，第 $i$ 个整数表示 $\mathrm{LCAS}(i)$ 的值对 $998,244,353$（一个大质数）取模后的结果。

5
3 1 2 1 3
1 2
1 3
3 4
3 5

109
0
18
0
0

10
1 1 4 5 1 4 1 9 1 9
1 2
1 3
1 4
2 5
2 6
5 7
3 8
3 9
9 10

972
33
99
0
2
0
0
0
10
0

提示

样例 1 解释

样例一当中的树如下。红色的是节点，蓝色的是点权。

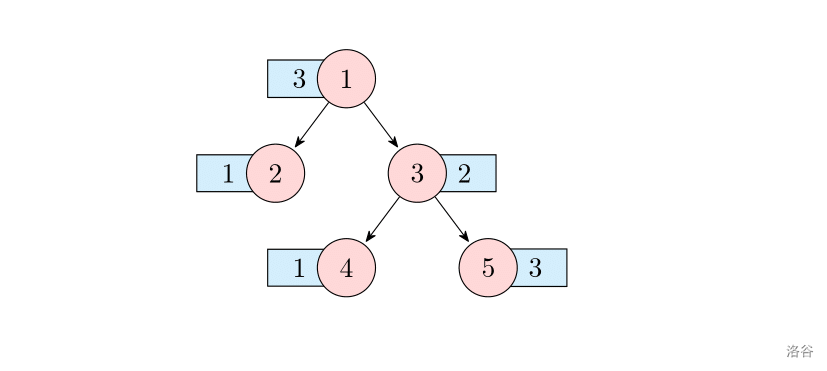
容易发现 $\mathrm{LCAS}(2)=\mathrm{LCAS}(4)=\mathrm{LCAS}(5)=0$。这里说明如何计算 $\mathrm{LCAS}(1)$ 和 $\mathrm{LCAS}(3)$。首先说明 $\mathrm{LCAS}(3)$：

• 以 $3$ 为根，那么有 $\mathrm{lca}(3,3,4)=\mathrm{lca}(3,3,5)=\mathrm{lca}(3,4,5)=3$，这部分的贡献是 $3\times w_3=6$。
• 以 $4$ 为根，那么有 $\mathrm{lca}(4,3,4)=\mathrm{lca}(4,4,5)=4,\mathrm{lca}(4,3,5)=3$，这部分的贡献是 $2\times w_4+1\times w_3=4$。
• 以 $5$ 为根，那么有 $\mathrm{lca}(5,3,5)=\mathrm{lca}(5,4,5)=5,\mathrm{lca}(5,3,4)=3$，这部分的贡献是 $2\times w_5+1\times w_3=8$。

因此，$\mathrm{LCAS}(3)=6+4+8=18$。下面计算 $\mathrm{LCAS}(1)$。

容易发现，在上图中，$1$ 出现了 $13$ 次，$2$ 出现了 $4$ 次，$3$ 出现了 $25$ 次，$4$ 出现了 $4$ 次，$5$ 出现了 $4$ 次。因此，$\mathrm{LCAS}(1)=3\times 13+1\times 4+2\times 25+1\times 4+3\times 4=109$。

样例 2 解释

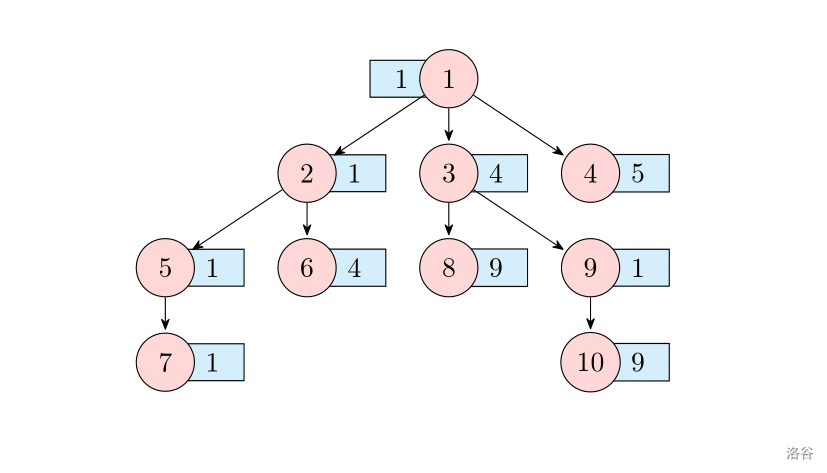
我有一个精妙绝伦的方法解释样例 $2$，可惜这里空白太小写不下。

本题输入量较大。请采用较快的读入方式。

数据范围及约定

特殊性质 $\textbf{A}$：保证第 $i$ 条边为 $u=i$，$v=i+1$。
特殊性质 $\textbf{B}$：保证第 $i$ 条边为 $u=1$，$v=i+1$。

对于全部数据，保证 $1\le n\le 10^6$，$0\le w_i<998,244,353$。