题目背景

这曾今有一个凄婉哀伤的故事，但是被出题人删档弄丢了。

题目描述

初始时，你有一个 $n$ 个结点 $m$ 条边的无向图 $G$，结点的编号依次为 $1,2,\cdots,n$。

现在将 $G$ 中所有 $m$ 条边依次编号，排成一个长度为 $m$ 边序列 $E=(e_1,e_2,\cdots,e_m)$，其中 $e_i=(u_i,v_i)$ 是一个二元组，表示一个连接 $u_i$ 与 $v_i$ 的无向边。

然后 Cirno 会给你 $q$ 个询问二元组 $( l, r )$，表示询问「如果只保留 $e_l,e_{l+1},\cdots e_r$ 这个区间内的边的话，图中的联通块的个数」。

时间紧急，你需要设计尽可能快的算法解决 Cirno 的询问，而且由于在某些情况下询问之间也许互相依赖，你的程序需要保持在线运行。

输入格式

第一行，四个整数，用空格隔开，分别表示 $n$, $m$, $q$, $t$, 其中 $t$ 表示强制在线参数，用于解密真实的询问。

接下来的 $m$ 行，其中第 $i$ 行包含两个整数 $u_i$ 与 $v_i$，用空格隔开，表示边序列 $E$。

再接下来 $q$ 行，每行两个整数 $l', r'$，用空格隔开，表示一组加密后的询问。

真实的询问二元组 $(l,r)$ 由以下方式解密

DecodeQuery( l', r', m, t, last_ans )
	(l, r) <- (l', r')
    IF t > 0 THEN 
        l <- (l + t * last_ans) Mod |E| + 1
        r <- (r + t * last_ans) Mod |E| + 1
    IF l' > r' THEN 
        Swap(l, r)
    RETURN (l, r)

其中 last_ans 表示上一次询问的答案，初始时 last_ans = 0.

输出格式

$q$ 行，表示每个询问的答案。

5 5 4 0
1 2
3 4
2 3
4 5
1 5
1 3
2 5
3 4
5 5

2
1
3
4

见附件中 sample2.in

见附件中 sample2.out

提示

样例解释

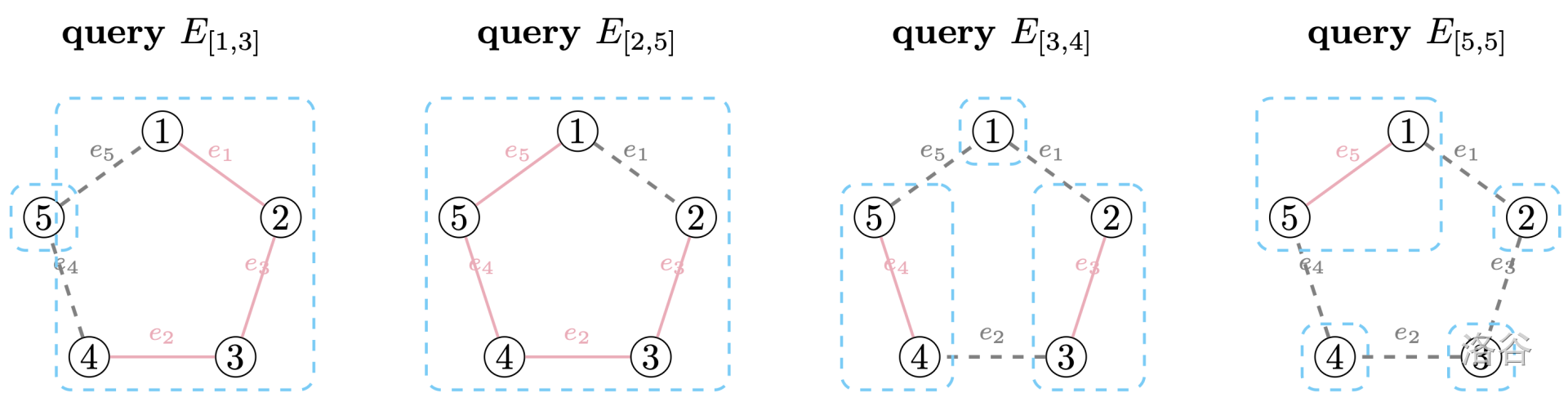
数据范围与约定

对于 $100\%$ 的数据保证，$1\le |V| \le 10^5, 1\le |E| \le 2\times 10^5, 1\le q \le 10^5, t \in \{0,1\}$。注意数据可能包含重边和自环。

子任务

Subtask1（$15$ points）：$|V|, |E|, q \le 5000$；

Subtask2（$25$ points）：$t = 0$；

Subtask3（$20$ points）：$|V| \le 10^4, |E|, q \le 3\times 10^4$

Subtask3（$40$ points）：无特殊限制。