题目背景

众所周知，庞氏骗局就是借新债还就债的骗术，隐瞒企业已经大开倒车的真相，保持虚假的增长。

题目描述

庞氏骗局源自于一个名叫查尔斯•庞兹的人。1919 年，他故弄玄虚，设计了一份假金融企划向大众兜售。借此，坑骗了成千上万的波士顿的长脖子鹿，套走了近 1500 万美金。

查尔斯•庞兹的骗局计划分为两部分，第一次他向 $K_1$ 名长脖子鹿展示了自己的创业计划，向每一头长脖子鹿要来了 $1$ 万元的投资。第二次他向 $K_2$ 名长脖子鹿展示了自己的创业计划，由于第二次需要填补第一次的亏空，所以向每一头长脖子鹿要来了 $2$ 万元的投资。

现在，查尔斯•庞兹拥有了 $K_1$ 份 $1$ 万元和 $K_2$ 份 $2$ 万元，他希望通过一种特定的方式消费从而躲避美国税务局（IRS）的追查。每一天，他都会选择两份钱，各消费 $1$ 万元。为了进一步减轻自己的嫌疑，他每天选择的两份钱不会与之前重复。他想知道，花光所有的钱，共有多少不同的方案集合，即方案内没有先后顺序，每一天不分先后。

例如：第一天选择了从 $(1,2)$ 两只长脖子鹿那里拿钱，第二天不能花 $(1,2)$ 两只长脖子鹿的钱，但可以从 $(2,3)$ 或 $(1,3)$ 这样的长脖子鹿组中拿钱。

方案数对 $10^9+7$ 取模。

输入格式

一行，两个正整数，$K_1,K_2$。

输出格式

一行，一个正整数，方案数。

2 2

2

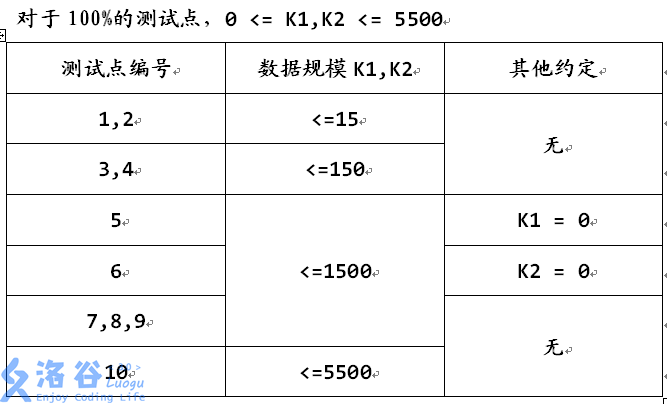
提示

样例解释

我们设 $1,2$ 号长颈鹿给了 $1$ 万元，$3,4$ 号长颈鹿给了 $2$ 万元。

方案一为这样的方案集合${(1,3),(3,4),(2,4)}$。

方案二位这样的方案集合${(1,4),(3,4),(2,3)}$。