#P4671. [BalticOI 2011] Polygon (Day2)
[BalticOI 2011] Polygon (Day2)
题目描述
A simple polygon with vertices is drawn on an infinite rectangular grid. For such a polygon, only neighboring edges touch at their common vertex; no other of its edges intersect or touch. All vertices of the polygon lie on grid points, i.e., vertices have integer coordinates.
Your task is to find the total length of grid line segments which lie strictly inside the given polygon (these line segments are highlighted in the drawings below).
输入格式
The first line of input contains a single integer , the number of vertices of the polygon. Each of the following lines contains two integers and , the coordinates of one vertex. The vertices are given either in clockwise or counterclockwise order. All vertices are distinct, but more than two consecutive vertices may lie on a line.
输出格式
The only line of output must contain a decimal number: the total length of grid line segments which lie strictly inside the given polygon.
3
5 1
2 4
1 1
10.0
5
0 0
-2 2
-2 -1
2 -2
2 0
12.5
提示
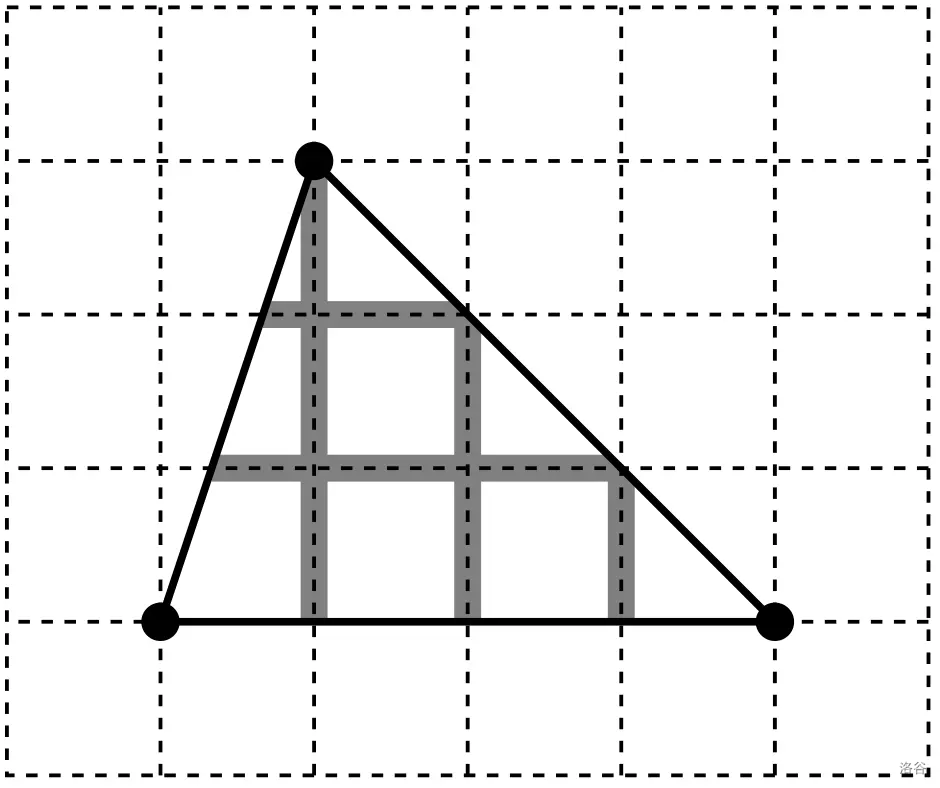
Sample Explanation 1
The length of horizontal lines is . The length of vertical lines is . The total length is .
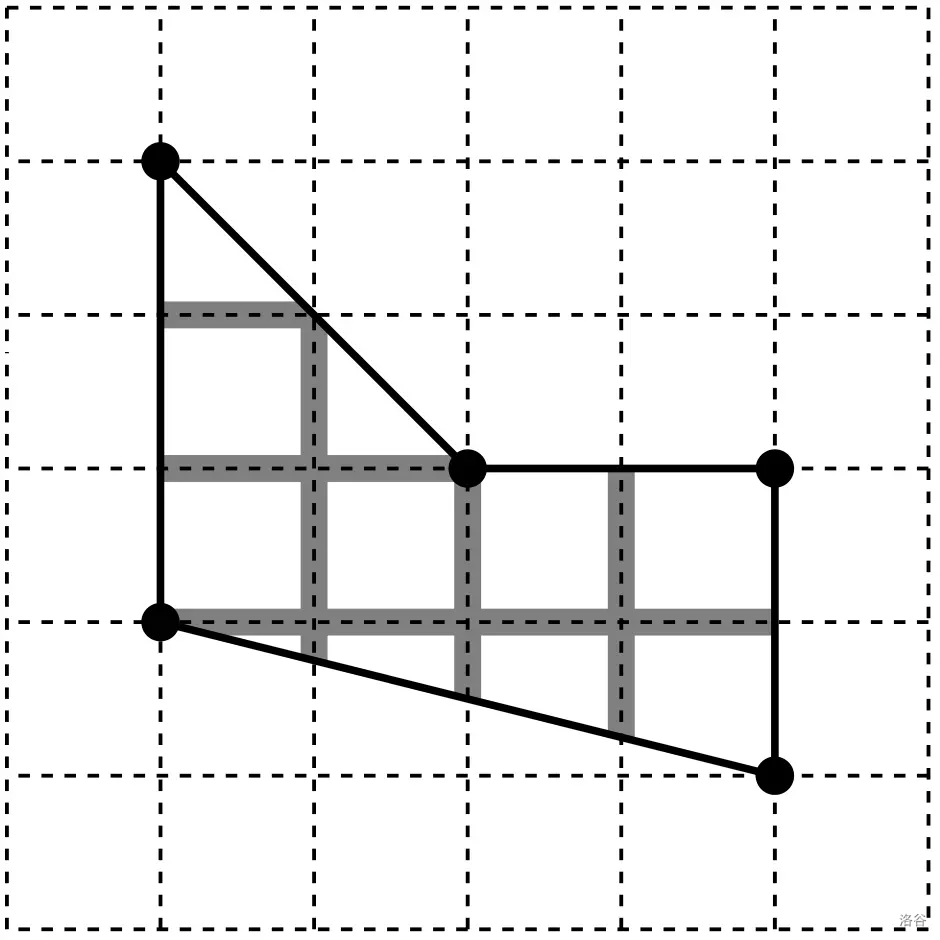
Sample Explanation 2
The length of horizontal lines is . The length of vertical lines is . The total length is .
数据范围
对于 的数据,多边形所有的边均在网格线上。
对于所有数据,$3 \le N \le 10^5,-5 \times 10^8 \le x,y \le 5 \times 10^8$。
