#P3790. 文艺数学题
文艺数学题
Background
After Xiao Y AK-ed Manhattan OI, CTSC, and APIO, he started studying math problems.
Problem Description
Xiao Y has an undirected graph with vertices and edges (possibly with multiple edges and self-loops), and each edge has a weight .
You need to compute the sum of the greatest common divisors of the edge weights over all spanning trees; see the sample for details.
Since the answer may be large, take it modulo .
Input Format
The first line contains two positive integers , denoting the number of vertices and the number of edges.
The next lines each contain three positive integers , denoting an edge connecting and with weight .
Output Format
Output a single integer: the answer modulo .
4 5
1 2 12
1 3 9
2 4 6
3 4 8
1 4 4
15
Hint
Explanation of Sample
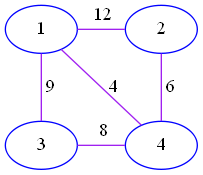
Obviously, this graph has different spanning trees.
Let denote the greatest common divisor of . Then the answer is
$\gcd(12,6,8)+\gcd(6,8,9)+\gcd(8,9,12)+\gcd(9,12,6)+\gcd(9,4,6)+\gcd(12,4,8)+\gcd(12,4,9)+\gcd(6,4,8)$
.
Constraints
For of the testdata, ;
For another of the testdata, ;
For another of the testdata, , and it satisfies ;
For another of the testdata, ;
For another of the testdata, ;
For of the testdata, .
Translated by ChatGPT 5
