题目描述

$$

分形是分数维的，介于 $2$ 维与 $3$ 维之间。完整的分形图往往具有有界的面积和无限的周长。为了探寻分形的奥秘，King 执着地进行着与众不同的研究。

首先他研究简单分形：平面上有一个半径为 $R_0$（$R_0 = 10^5$）的圆，圆心处于坐标原点，它与若干个半径为 $R_1$ 的圆外切，每个半径为 $R_1$ 的圆与若干个半径为 $R_2$ 的圆外切，……，每个半径为 $R_i$ 的圆与若干个半径为 $R_{i+1}$ 的圆外切。任意两圆不相交、不重叠、不内含、不内切。半径为 $R_i$ 的圆只可能与半径为 $R_{i-1}$ 或 $R_{i+1}$ 的圆外切，$i > 0$ 时恰与 1 个半径为 $R_{i-1}$ 的圆外切。

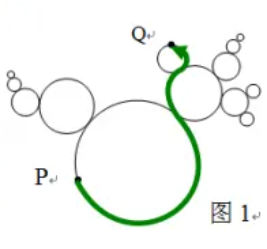
作为基础，他先研究有限层的简单分形，即只由半径为 $R_0 \sim R_n$ 的圆构成的 $n + 1$ 层分形。图 $1$ 是一个 $5$ 层简单分形。由于只有有限层，所以此图的边界为有限长。

King 在边界上找出了与分形图的性质有关的若干个点对（$P_i, Q_i$），从 $P_i$ 到 $Q_i$，最短的光滑路径的长度是多少（如图 $1$ 中的加粗曲线）。

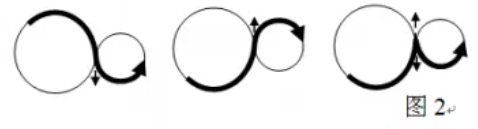
光滑路径是指：路径在两圆公切点拐弯时切线方向保持不变。图 $2$ 中左边两段（加粗）路径是光滑的，而右边的（加粗）路径不光滑。

输入格式

$$

第一行为 $3$ 个整数 $n, m, t$。其中 $m$ 表示圆的个数（并且圆的编号为 $1 \sim m$），$t$ 为特殊点对数。

第二行为 $n$ 个正整数 $R_1 \sim R_n$。

接下来的 $m$ 行表示各个圆，每行有 $4$ 个数 $X_i, Y_i, S_i, F_i$, $(X_i, Y_i)$ 是圆 $i$ 的圆心位置，圆 $i$ 的半径是 $R_{S_i}$，与圆 $i$ 相切的尺寸更大的圆的编号是 $F_i$，$X_i$ 和 $Y_i$ 可能是实数。

再接下来的 $t$ 行表示各个特殊点对，每行有 $4$ 个数 $P_{i,tW}, P_{i,tA}, Q_{i,tW},Q_{i,tA}$，用于描述一个特殊点对 $(P_i, Q_i)$ 的位置：

• $P_{i,tW}$ 表示点 $P_i$ 处于 $P_{i,tW}$ 这个圆上，并且以此圆圆心为原点的幅角为 $P_{i,tA}$。
• $Q_{i,tW}$ 表示点 $Q_i$ 处于 $Q_{i,tW}$ 这个圆上，并且以此圆圆心为原点的幅角为 $Q_{i,tA}$。

输出格式

$$

对于每个特殊点对，输出一行一个整数，表示最短长度除以 $\pi$ 后四舍五入保留整数的结果。

1 3 3
50000
0 0 0 0
150000 0 1 1
0 150000 1 1
3 5.497787 	  2 2.356194
3 1.570796 	  2 0.0
3 0.0         2 1.570796

175000
150000
200000

提示

对于 $50\%$ 的数据：

• $m \le 300$。
• $t \le 1000$。

对于 $100\%$ 的数据：

• $1 \le n < m \le 3000$。
• $1 \le t \le 10^5$。
• $2 \le R_n < R_{n-1} < \ldots < R_1 < R_0$。
• $R_{i-1} - R_i \ge 2$。
• $R_0 = 10^5$。
• $S_0 = -1$。
• $X_1 = Y_1 = F_1 = S_1 = 0$。
• $-3 \times 10^8 \le X_i, Y_i \le 3 \times 10^8$。
• $0 \le S_i \le n$。
• $1 \le F_i \le m$。
• $F_i \ne i$。
• $S_{F_i} = S_i-1$。
• $1 \le P_{i,tW},Q_{i,tW} \le m$。
• $P_{i,tW} \ne Q_{i,tW}$。
• $0 \le P_{i,tA},Q_{i,tA} < 2\pi$。
• 所有的圆之间要么外切要么相离。
• 所有特殊点都不是切点。
• 一个圆最多与 $10$ 个圆外切。
• 所有实数最多保留 $6$ 位小数。