#P15239. [NHSPC 2025] Chomp!
[NHSPC 2025] Chomp!
题目描述
是一个经典的两人游戏。起始时有一片由 块大小为 的小块巧克力连为一片的巧克力,形状如 的二维数组(其中 为行, 为列),而最左下角的那一小块非常苦涩,大家都想避开。游戏的玩法为轮流拿走巧克力小块,方式是先从剩下来的巧克力挑一小块,并把其右上方(含正上方及正右方)所有小块同时拿掉。到最后谁拿到最左下角的那一小块便输了。
例如起始时有 的一片巧克力:
:::align{center}
 :::
:::
若玩家一选择了 那一小块,则连带 的那些小块也会被拿掉:
:::align{center}
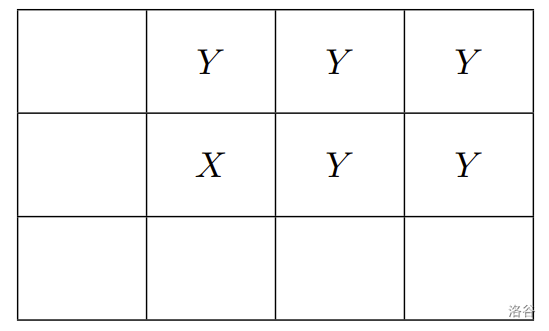 :::
:::
接着由玩家二从剩下的巧克力块选择。若玩家二此时选择了 那一小块,则连带 的那些小块也会被拿掉:
:::align{center}
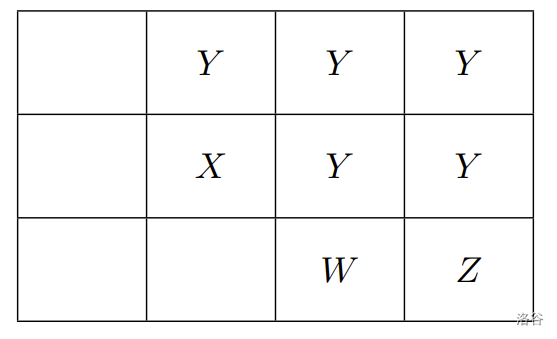 :::
:::
按照以上规则,我们不难证明,在游戏中所出现的任何情形,如从左至右输出每一列 (column) 的巧克力小块数,其结果必为一单调递减 (monotonic decreasing) 数列,且对应此数列之形状唯一。如上例的最终状态,其可以数列 表示。
在此题目中,我们针对 大小巧克力的 游戏中出现的各种情况进行分析,目的是计算在当前的情况下,先行者是否有获胜的走法。我们假设游戏双方皆绝顶聪明,会采取最好的游玩策略来让自己获胜。若先行者能获胜,我们输出在目前情况下有多少种可以获胜的第一步选择,并把这些选择枚举出来;反之,则输出 。这里,我们将下面数上来第 行、左边数过来第 列的小块巧克力编号为 ,满足左下角为 ,右上角为 。
输入格式
$$\begin{aligned} &t \\ &n_1 \; p_1 \; q_1 \; r_1 \\ &\vdots \\ &n_t \; p_t \; q_t \; r_t \end{aligned}$$- 代表总共有 笔询问。
- 代表第 笔询问的巧克力总列数。
- 代表第 笔询问的状态为从左至右先有 列为 小块巧克力,接着有 列为 小块巧克力,再有 列为 小块巧克力。
输出格式
$$\begin{aligned} &c_1 \\ &x_{1,1} \; y_{1,1} \; \dots \; x_{1,c_{1}} \; y_{1,c_{1}} \\ &\vdots \\ &c_t \\ &x_{t,1} \; y_{t,1} \; \dots \; x_{t,c_{t}} \; y_{t,c_{t}} \end{aligned}$$- 代表在第 笔询问的状态下,先行者可以获胜的第一步选择数。若先行者无法获胜,则 。
- 代表第 笔询问中,第 个可以作为先行者获胜的第一步选择的小块巧克力编号。若 ,请依 值小到大排序编号,若 值相同则依 值小到大排序编号。
4
1 0 0 1
10 1 0 9
3 1 2 0
3 1 1 1
0
1
1 4
2
1 3 2 2
3
1 3 2 2 3 1
1
100 67 22 11
3
1 100 2 59 3 18
提示
数据限制
- 。
- 。
- 。
- 。
- 输入的数皆为整数。
评分说明
本题共有三组子任务,条件限制如下所示。 每一组可有一或多笔测试资料,该组所有测试资料皆需答对才会获得该组分数。
| 子任务 | 分数 | 额外输入限制 |
|---|---|---|
| 1 | 20 | ,。 |
| 2 | 37 | 。 |
| 3 | 43 | 无额外限制。 |
