#P15238. [NHSPC 2025] 電動車充電規劃問題
[NHSPC 2025] 電動車充電規劃問題
题目描述
小明买了一台电动车,其电池容量为 。小明知道电动车的初始电量 ,他要规划从起点开到终点的路线,使得所需的充电费用越少越好。电动车在一些路段会耗电(如平路或是上坡),在一些路段会充电(如下坡)。这些充电路段是不会收费的。我们用一个有向图表示地图,边的权重代表电动车开过此边会让电量增加或减少,如果开过此边会充电,则边的权重为一个正数,反之如果开过此边会耗电,则边的权重为一个负数。我们假设图没有正环。
电动车在行驶时,电量需要永远大于等于 ,而且无论充电量多大,电量最多为 。更明确地说,令 为电动车目前电量,并考虑一个权重为 的边:如果 非负数,则电动车一定可以开过此边(即使电量 ),且剩余电量为 ;如果 是负数,且 ,则电动车可以开过此边,且开过此边后的剩余电量为 ;然而,如果 ,则电动车无法开过此边。
地图上有一些节点是充电站,小明可以经过多个充电站,因为充电要花时间找充电桩,小明决定路途中最多只用一个充电站充电。充电一单位的价格是一块钱,小明的目标是花最少的钱到达目的地。
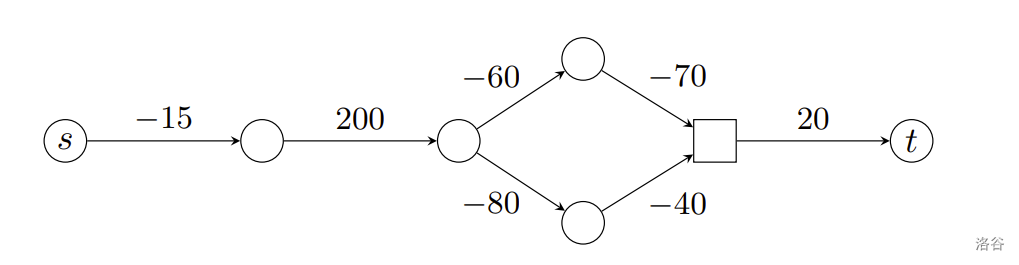
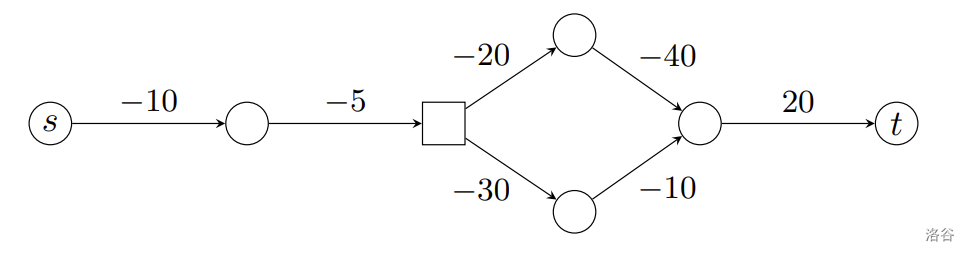
举例来说,考虑以下三个图,我们用方形节点代表充电站,圆形节点则无法充电。假设电池容量 ,起点为 ,终点为 ,且初始电量为 。
在下图中,电动车可以从 抵达 ,且最小充电费用为 。
:::align{center}
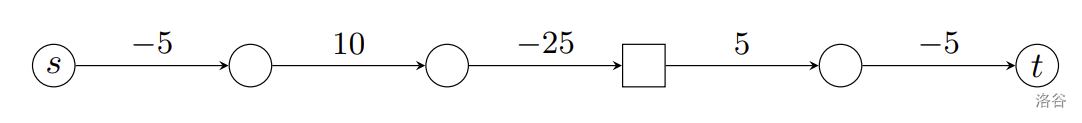 :::
:::
在下图中,电动车无法从 抵达 。
:::align{center}
 :::
:::
在下图中,电动车可以从 抵达 ,且最小充电费用为 。
:::align{center}
 :::
:::
输入格式
$$\begin{aligned} &n \; m \; s \; t \\ &B \; b \\ &u_1 \; v_1 \; w_1 \\ &u_2 \; v_2 \; w_2 \\ &\vdots \\ &u_m \; v_m \; w_m \\ &g \; p_1 \; p_2 \; \cdots \; p_g \end{aligned}$$- 为节点数。
- 为边数。
- 为起点编号。
- 为终点编号。
- 为电池容量。
- 为电池初始电量。
- 代表图中有一个边由节点 至节点 ,且权重为 。
- 为充电站个数。
- 为第 个充电站的节点编号。
输出格式
- 代表最少所需的充电费用。如果不存在路径抵达终点,则 。
6 5 1 6
100 20
1 2 -5
2 3 10
3 4 -25
4 5 5
5 6 -5
1 4
0
7 7 1 7
100 20
1 2 -15
2 3 200
3 4 -60
3 5 -80
4 6 -70
5 6 -40
6 7 20
1 6
-1
7 7 1 7
100 20
1 2 -10
2 3 -5
3 4 -20
3 5 -30
4 6 -40
5 6 -10
6 7 20
1 3
35
7 7 1 7
100 60
1 2 -10
2 3 -5
3 4 -20
3 5 -30
4 6 -40
5 6 -10
6 7 -5
0
0
提示
数据限制
- 。
- 。
- 。
- 。
- 。
- ,且 。
- 。
- 。
- 。
- 保证图没有正环。
- 输入的数皆为整数。
评分说明
本题共有四组子任务,条件限制如下所示。 每一组可有一或多笔测试资料,该组所有测试资料皆需答对才会获得该组分数。
| 子任务 | 分数 | 额外输入限制 |
|---|---|---|
| 1 | 15 | 输入满足所有路段都不会充电,即 , 且没有充电站,即 。 |
| 2 | 30 | 输入满足所有路段都不会充电,即 。 |
| 3 | 23 | 输入满足没有充电站,即 。 |
| 4 | 32 | 无额外限制。 |
