题目描述

为了逃离圣诞集市的喧嚣，你计划前往威尼斯旅行，欣赏其美丽的运河与众多桥梁。不幸的是，似乎并非只有你一人有此打算，而且威尼斯最近决定为此乐趣收费。因此，你认为每座桥只经过一次就已足够。幸运的是，仅通过街道（不经过任何桥梁）即可从任一地点到达任何其他地点。有趣的是，仅使用街道前往任何其他地点恰好只有一条路径。

在收集完所有这些信息后，现在剩下的就是规划一条每条桥梁恰好经过一次的路线。为了保持趣味性，你还希望每条街道最多使用一次。最短可能路线的长度是多少？注意你的游览可以从任意地点开始，但必须回到起点结束。

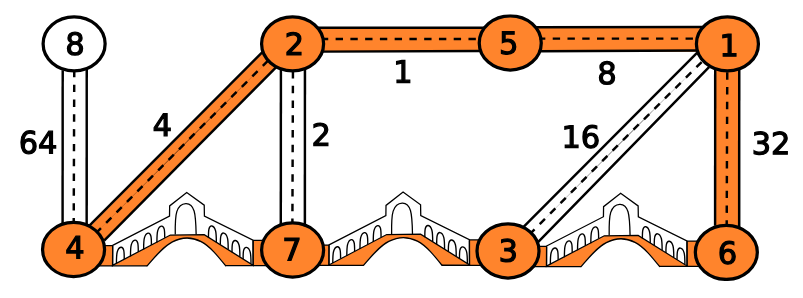
图 C.1：样例输入 1 的图示，展示了一条长度为 $45$ 的路线。

输入格式

输入包含：

• 一行，一个整数 $n$（$3 \le n \le 10^5$），表示威尼斯的地点数量。
• $n-1$ 行，每行三个整数 $a, b$ 和 $w$（$1 \le a, b \le n, a \ne b, 1 \le w \le 10^6$），表示每条街道的起点、终点及其长度。
• 一行，一个整数 $m$（$1 \le m \le 5 \cdot 10^5$），表示威尼斯的桥梁数量。
• $m$ 行，每行两个整数 $a$ 和 $b$（$1 \le a, b \le n, a \ne b$），表示每座桥梁连接的起点和终点。

桥梁很短，因此长度为零。

保证不使用任何桥梁即可从任一地点到达任何其他地点。此外，没有桥梁直接连接由街道直接相连的两个地点，且所有桥梁连接的地点对互不相同。最后，保证至少存在一条路线可以恰好经过每座桥梁一次，且每条街道最多使用一次。

输出格式

输出一条经过所有桥梁且每条街道最多使用一次的最短路线的长度。

8
5 1 8
5 2 1
2 7 2
4 2 4
3 1 16
1 6 32
8 4 64
3
7 4
3 6
3 7

45

5
1 3 1
2 1 3
1 4 3
5 1 7
4
3 2
4 5
2 5
3 4

0