题目描述

Kiara studies an odd species of birds which travel in a very peculiar way. Their movements are best explained using the language of graphs: there exists a directed graph $G$ where the nodes are trees, and a bird can only fly from a tree $T_a$ to $T_b$ when $(T_a, T_b)$ is an edge of $G$.

Kiara does not know the real graph $G$ governing the flight of these birds but, in her previous field study, Kiara has collected data from the journey of many birds. Using this, she has devised a graph $P$ explaining how they move. Kiara has spent so much time watching them that she is confident that if a bird can fly directly from $a$ to $b$, then she has witnessed at least one such occurrence. However, it is possible that a bird flew from $a$ to $b$ to $c$ but she only witnessed the stops $a$ and $c$ and then added $(a,c)$ to $P$. It is also possible that a bird flew from $a$ to $b$ to $c$ to $d$ and she only witnessed $a$ and $d$, and added $(a,d)$ to $P$, etc. To sum up, she knows that $P$ contains all the edges of $G$ and that $P$ might contain some other edges $(a,b)$ for which there is a path from $a$ to $b$ in $G$ (note that $P$ might not contain all such edges).

For her next field study, Kiara has decided to install her base next to a given tree $T$. To be warned of the arrival of birds on $T$, she would also like to install detectors on the trees where the birds can come from (i.e. the trees $T'$ such that there is an edge $(T', T)$ in $G$). As detectors are not cheap, she only wants to install detectors on the trees $T'$ for which she is sure that $(T', T)$ belongs to $G$.

Kiara is sure that an edge $(a,b)$ belongs to $G$ when $(a,b)$ is an edge of $P$ and all the paths in $P$ starting from $a$ and ending in $b$ use the edge $(a,b)$. Kiara asks you to compute the set $S(T)$ of trees $T'$ for which she is sure that $(T', T)$ is an edge of $G$.

输入格式

The input describes the graph $P$. The first line contains three space-separated integers $N$, $M$, and $T$: $N$ is the number of nodes of $P$, $M$ is the number of edges of $P$ and $T$ is the node corresponding to the tree on which Kiara will install her base.

The next $M$ lines describe the edges of the graph $P$. Each contains two space-separated integers $a$ and $b$ ($0 \leq a, b < N$ and $a \neq b$) stating that $(a,b) \in P$. It is guaranteed that the same pair $(a,b)$ will not appear twice.

输出格式

Your output should describe the set $S(T)$. The first line should contain an integer $L$, which is the number of nodes in $S(T)$, followed by $L$ lines, each containing a different element of $S(T)$. The elements of $S(T)$ should be printed in increasing order, with one element per line.

3 3 2
0 1
0 2
1 2

1
1

6 8 2
0 1
0 2
1 2
2 0
2 3
3 4
4 2
2 5

2
1
4

提示

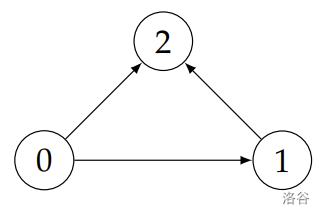
Sample Explanation 1

The graph corresponding to this example is depicted on the right. The node $1$ belongs to $S(2)$ because the (only) path from $1$ to $2$ uses $(1,2)$. The node $0$ does not belong to $S(2)$ because the path $0 \to 1 \to 2$ does not use the edge $(0,2)$.

:::align{center} :::

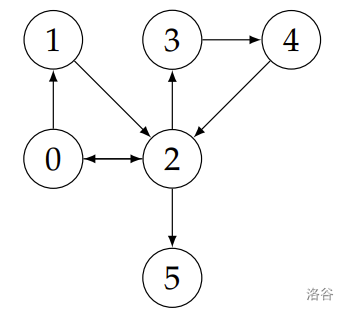
Sample Explanation 2

The graph corresponding to this example is depicted on the right. For the same reason as in Sample 1, the node $0$ does not belong to $S(2)$ while $1$ does. The nodes $3$ and $5$ do not belong to $S(2)$ because we do not have edges $(3,2)$ or $(5,2)$. Finally $4$ belongs to $S(2)$ because all paths from $4$ to $2$ use the edge $(4,2)$.

:::align{center} :::

Limits

• $1 \leq N, M \leq 100\,000$;
• $0 \leq T < N$.