题目描述

Tania is a marine biologist. Her goal is to measure the impact of climate change on the population of Macaroni penguins. As most species of penguins, Macaroni penguins live in the southern hemisphere, near Antarctica. Tania is primarily focused on the population of Macaroni penguins near the “Îles Nuageuses” (in English, “Cloudy Islands”).

During summer, the ice around the islands melt and the islands becomes too small to host all the birds. Some penguins live on the icebergs floating around. For her study, Tania needs to measure the area of those icebergs.

Using satellite imagery and image recognition, Tania has obtained a map of the icebergs and your goal is to measure their area. The island studied by Tania is quite small and the Earth can locally be approximated as a flat surface. Tania’s map thus uses the usual 2D Cartesian coordinate system, and areas are computed in the usual manner. For instance, a rectangle parallel to the axes defined by the equations $x_1 \leq x \leq x_2$ and $y_1 \leq y \leq y_2$ has an area of $(x_2 - x_1) \times (y_2 - y_1)$.

In Tania’s representation, an iceberg is a polygon represented by its boundary. For each iceberg Tania has noted the sequence of points $p_1, \ldots, p_k$ defining the border of the iceberg. The various icebergs never touch each other and they never overlap. Furthermore the boundary $p_1, \ldots, p_k$ of an iceberg is always a “simple” polygon, i.e. no two segments in $[p_1; p_2], \ldots, [p_k; p_1]$ cross each other.

输入格式

The input consists of the following lines:

• on the first line, an integer $N$, describing the number of polygons;
• then $N$ blocks of lines follow, each describing a polygon and composed of:
  • on the first line, an integer $P$, the number of points defining the polygon border,
  • on the next $P$ lines, two space-separated integers $x$ and $y$, the coordinates of each border point.

输出格式

The output should contain a single integer: the total area rounded to the nearest integer below. In other words, the output should be a single line containing a single integer $I$ such that the total area $A$ of the polygons described in the input is comprised between $I$ included and $I+1$ excluded ($I \leq A < I+1$).

1
4
0 0
1 0
1 1
0 1

1

2
5
98 35
79 90
21 90
2 36
50 0
3
0 0
20 0
0 20

6100

提示

Sample Explanation 1

This sample has a unique iceberg, which is a square of side 1.

Sample Explanation 2

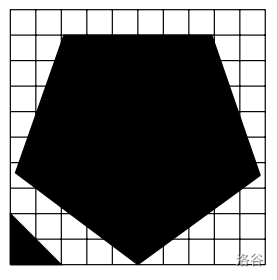
In this sample (depicted on the right) there are two icebergs, a triangle of area $200$ and a pentagon of area $5900.5$.

:::align{center} :::

Limits

• The number $N$ of polygons is such that $1 \leq N \leq 1000$.
• Each polygon is described by $P$ points with $3 \leq P \leq 50$.
• All coordinates are such that $0 \leq x, y \leq 10^6$.