题目描述

You are a Roman general setting up a defence fort against the Barbarians. You only know how to build straight walls, so your fort is going to be polygon-shaped.

Due to the shape of the land, which has multiple hills located at all the integer coordinates, you know that the enemy artillery can only be installed in very specific ways, and that higher positions inside your fort are more vulnerable, which means that:

• all the vertices of the polygon must have integer coordinates between $1$ and $10^9$ (inclusive);
• $N$ known points $(x_i, y_i)$, $i = 1, \ldots, N$, with integer coordinates between $1$ and $10^9$ (inclusive), initially given, must be among the vertices of the polygon;
• no point with integer coordinates can be located strictly inside the polygon, as it would be vulnerable to the enemy artillery otherwise;
• the polygon needs to be simple¹ (obviously, the fort needs to be closed, and you don't know how to build intersecting walls).

In addition, due to the cost of building this fort and the limited materials, you can only afford to build a polygon with a number of vertices smaller than or equal to $3N$.

It can be shown that such a polygon always exists.

¹A simple polygon is a polygon formed by a single closed path that does not intersect itself or overlap itself.

输入格式

The first line contains the integer $N$. The next $N$ lines contain two space-separated integers $x_i$, $y_i$, the points that must be among the vertices of the polygon.

输出格式

The first line should contain $K$, the number of vertices of the polygon.

The next $K$ lines should contain two space-separated integers $x'_i$, $y'_i$, the coordinates of the vertices of the polygon. They must be in an order that forms a closed and non-intersecting path that defines the outline of the polygon.

If there are multiple solutions, you can output any of them.

4
1 1
1 3
3 1
3 3

5
1 1
3 1
3 3
2 2
1 3

提示

Sample Explanation

The following is a possible solution for the sample input:

:::align{center} :::

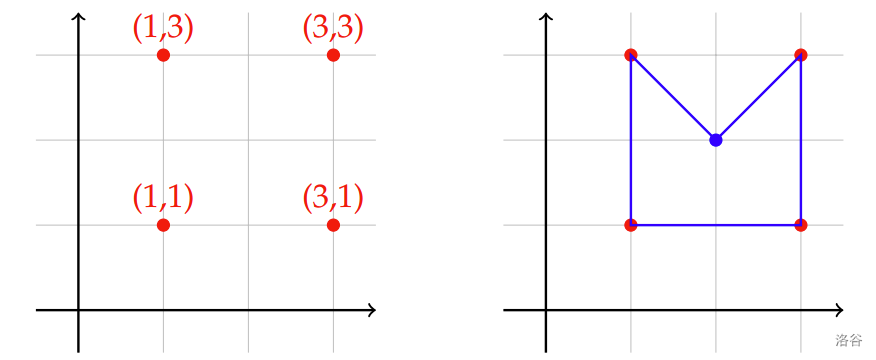On the other hand, the following polygons are not valid solutions:

:::align{center} :::

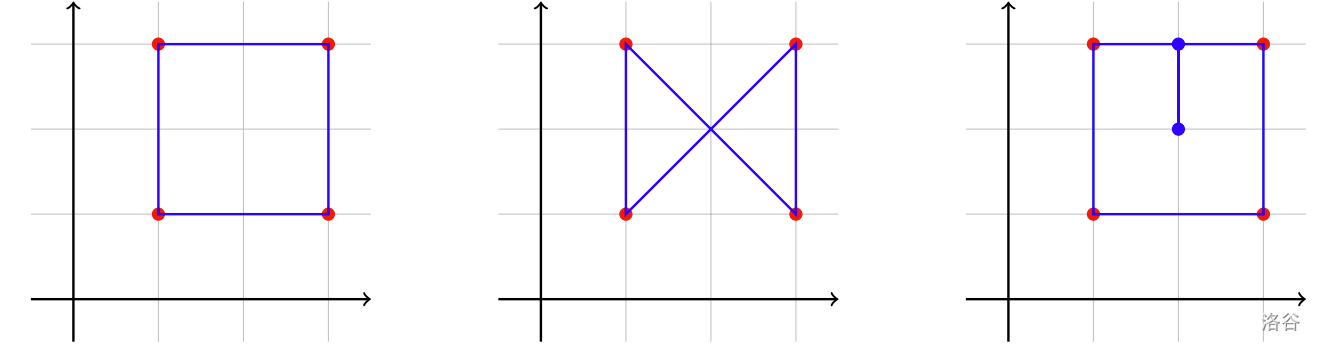Limits

• $3 \leq N \leq 1000$;
• $1 \leq x_i \leq 10^9$ for $i = 1, \ldots, N$;
• $1 \leq y_i \leq 10^9$ for $i = 1, \ldots, N$;
• All $(x_i, y_i)$ are unique;
• $1 \leq x'_i \leq 10^9$ for $i = 1, \ldots, K$;
• $1 \leq y'_i \leq 10^9$ for $i = 1, \ldots, K$;
• All $(x'_i, y'_i)$ must be unique.