题目描述

:::align{center} :::

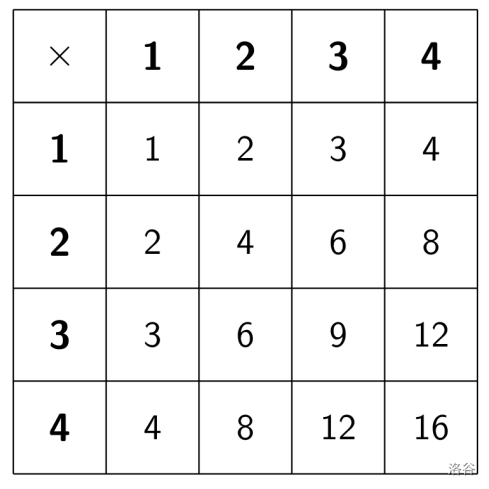
You are playing the sandbox game Mathcraft. Each crafting table of level $k$ can produce all possible products obtained by multiplying two numbers between 1 and $k$.

If you unroll the $k$-th crafting table, you get the array $[1 \cdot 1, 1 \cdot 2, \dots, 1 \cdot k, 2 \cdot 1, 2 \cdot 2, \dots, 2 \cdot k, \dots, k \cdot 1, k \cdot 2, \dots, k \cdot k]$. For example, for $k = 4$, the unrolled table is $[1, 2, 3, 4, 2, 4, 6, 8, 3, 6, 9, 12, 4, 8, 12, 16]$.

Your friend Bob crafted a (contiguous) subarray of one unrolled crafting table. This subarray is $a_1, a_2, \dots, a_n$.

You want to know how skilled Bob is, so you want to find the minimum possible level of his crafting table. Specifically, you want to determine the smallest $k$ such that $a_1, a_2, \dots, a_n$ appears as a subarray of the $k$-th unrolled table.

An array $b$ is a subarray of an array $c$ if $b$ can be obtained from $c$ by deleting several (possibly zero or all) elements from the beginning and several (possibly zero or all) elements from the end.

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1 \le t \le 500$). The description of the test cases follows.

The first line of each test case contains a single integer $n$ ($2 \le n \le 100$) — the length of the array $a_1, a_2, \dots, a_n$.

The second line of each test case contains $n$ integers $a_1, a_2, \dots, a_n$ ($1 \le a_i \le 10^9$).

Note that there are no constraints on the sum of $n$ over all test cases.

输出格式

For each test case, output a single line containing an integer: the smallest crafting table level $k$ such that the array $a_1, a_2, \dots, a_n$ appears as a contiguous subarray of the $k$-th unrolled table. For the given input, such a $k$ always exists.

4
4
4 6 8 10
6
8 3 6 9 12 4
5
30 40 50 60 70
4
1 2 2 4

5
4
10
2

提示

Explanation of sample 1.

In the first test case, the array $[4, 6, 8, 10]$ is a subarray of the 5-th unrolled table, which is $[1, 2, 3, 4, 5, 2, 4, 6, 8, 10, \dots, 5, 10, 15, 20, 25]$. There is no smaller valid $k$, so the answer is $5$.

In the second test case, the array $[8, 3, 6, 9, 12, 4]$ is a subarray of the 4-th unrolled table, which is $[1, 2, 3, 4, 2, 4, 6, 8, 3, 6, 9, 12, 4, 8, 12, 16]$.