题目描述

The Treeland subway system consists of $N$ stations connected by $N-1$ bidirectional tunnels. The tunnels are arranged in such a way that it is always possible to travel between any two stations. The system is already considered to be the most efficient in the country: there are trains between every pair of stations in the system.

Alejandro, from the subway improvement department, has been tasked with making the system even better and more attractive for passengers and businesses. To that end, the department collected $P$ proposals from companies. Each proposal is either to sponsor some station (basically, add a sign with the name of the company on the station), or to open a business at some station (a restaurant, a store, or anything like this). Notice that there is no restriction on the number of proposals that can be accepted for each station.

Companies willing to open businesses in the system, though, informed that they will withdraw their proposals unless the station $X$ where their business is located, is either a sponsored station or there is a train between two sponsored stations that goes through $X$. Of course, Alejandro does not want to select proposals that will later be withdrawn. Thus, he will make sure to select a set of proposals such that no proposal in the set will be withdrawn. He calls such a set a valid set of proposals.

The figure below shows sponsored stations in red/dashed circles and businesses in blue/dotted circles. The set of proposals in (a) is valid because the business proposal for station 3 is located exactly on the path between the two sponsored stations 2 and 4. The set of proposals in (b) is also valid, because the business proposal for station 1 is located exactly on a sponsored station. On the contrary, the set of proposals in (c) is not valid: even though the business proposal for station 3 is located on a path between two sponsored stations, the business proposal for station 5 is not.

:::align{center} :::

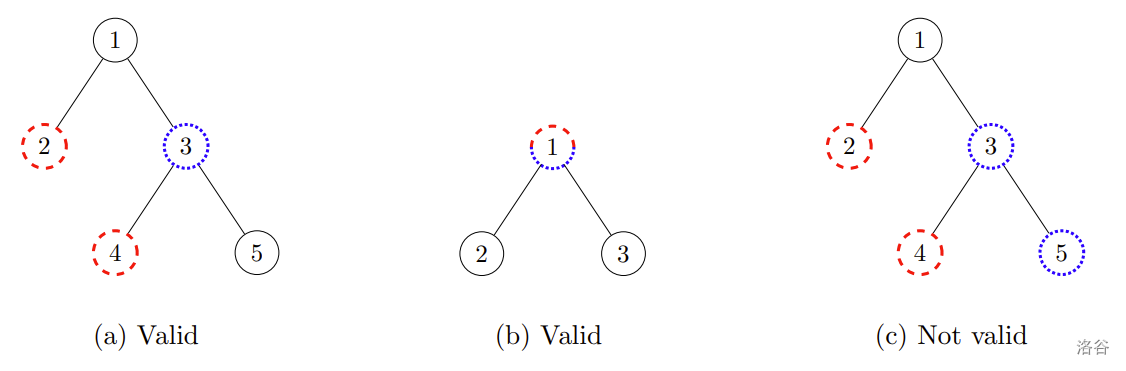To choose a valid set, Alejandro took the $P$ proposals (each one described on a piece of paper), and numbered them from $1$ to $P$. Now he wants to select a contiguous range of proposals that form a valid set. More precisely, he wants to pick two integers $i$ and $j$, with $1 \le i \le j \le P$, such that proposals $i, i+1, \dots, j$ form a valid set; besides, he wants the set to be as large as possible. Alejandro is not sure about which should be the initial proposal $i$ in the range he will select. Help him compute for each $i$ from $1$ to $P$, the size of the largest contiguous range of proposals that form a valid set, starting at proposal $i$.

输入格式

The first line contains an integer $N$ ($2 \le N \le 10^5$) indicating the number of stations in the subway system. Each station is identified by a distinct integer from $1$ to $N$.

Each of the next $N-1$ lines contains two integers $U$ and $V$ ($1 \le U, V \le N$ and $U \ne V$), representing that there is a bidirectional tunnel between stations $U$ and $V$. It is guaranteed that it is possible to go from any station to any other station using the tunnels.

The next line contains an integer $P$ ($1 \le P \le 10^5$) denoting the number of proposals submitted by companies. Each proposal is identified by a distinct integer from $1$ to $P$.

The $i$-th of the next $P$ lines describes proposal $i$ with a character $C$ and an integer $X$ ($1 \le X \le N$). For a sponsoring proposal $C$ is the lowercase letter "s", while for a business proposal it is the lowercase letter "b"; in both cases $X$ is the corresponding station. Notice that each station can have an arbitrary number of proposals of any type.

输出格式

Output $P$ lines. The $i$-th line must contain an integer indicating the size of the largest valid set of contiguous proposals whose initial proposal is $i$.

6
2 1
1 3
3 5
5 6
4 3
8
b 1
s 2
b 6
s 3
b 4
s 5
b 3
s 4

0
1
0
5
4
3
0
1

7
4 2
2 1
1 3
3 6
5 2
3 7
6
s 4
b 5
b 6
s 7
b 2
s 3

1
0
0
1
0
1

2
1 2
5
s 1
b 1
s 1
b 1
s 1

5
4
3
2
1