题目描述

Vasylko was given cubes with numbers from $1$ to $n$. One cube had the number $n$, two cubes had the number $n-1$, and so on, with $n-1$ cubes having the number $2$, and $n$ cubes having the number $1$.

He arranged the cubes in a square frame without a top boundary, so that all cubes were placed below the diagonal that runs from the top left corner to the bottom right corner. In the first column on the left, there are $n$ cubes with the number $1$; in the second column, there are $n-1$ cubes with the number $2$... in the $n$-th column, there is one cube with the number $n$. That is, in the $i$-th column, there are $n-i+1$ cubes with the number $i$.

:::align{center}

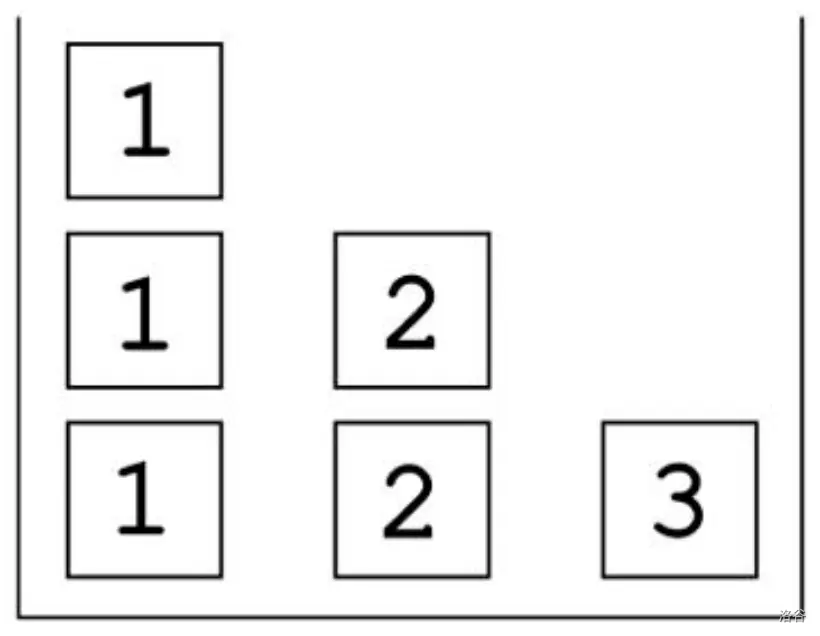
Initial state :::

Vasylko wanted to rearrange them so that all cubes were positioned below the $\textbf{opposite diagonal}$. Thus, in the first row from the bottom, there should be $n$ cubes with the number $1$; in the second row, there should be $n-1$ cubes with the number $2$... in the $n$-th row, there should be one cube with the number $n$. That is, in the $i$-th row, there should be $n-i+1$ cubes with the number $i$.

:::align{center}

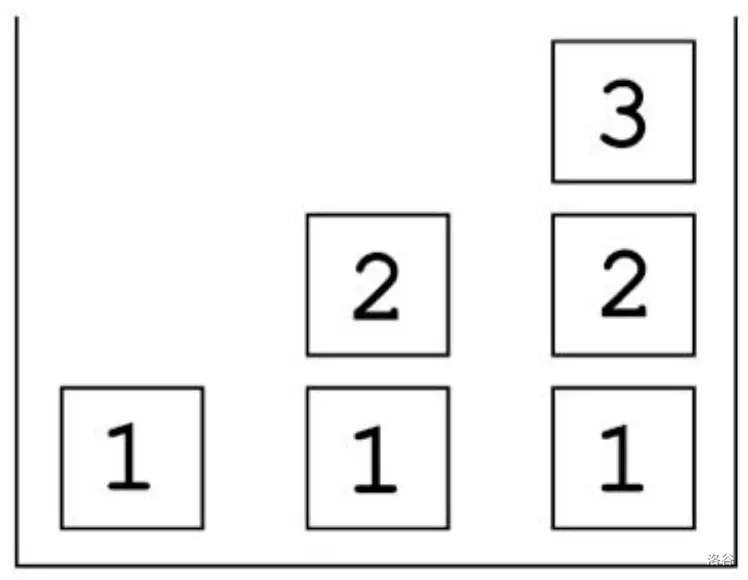
Final state :::

He also decided that he would only move cubes from the top of one column to the top of another (not necessarily adjacent). Help him do this in the most efficient way --- find the minimum number of moves he needs and output which moves Vasylko should make.

$\textbf{You can earn partial points; see details below.}$

输入格式

The first line contains one integer $n$ $(3 \le n \le 1000)$ --- the size of the square.

输出格式

In the first line, output one integer $k$ ($1 \leq k \leq 10^6$) --- the minimum number of moves needed to rearrange the cubes.

In each of the following $k$ lines, output two integers $a$ and $b$ ($1 \leq a, b \leq n$; $a \neq b$), where $a$ is the column number from which you take a cube, and $b$ is the column number to which you place the cube.

3

8
3 2
1 3
2 1
2 3
1 3
2 3
1 2
3 2

提示

First, we will place the last column. Therefore, the only first move to rearrange the cubes in the minimum number of moves may be to move $3$ from the third column to the second, because otherwise we will not be able to place $1$ at the beginning of the third column if we do not move $3$ or do not move it to the second column.

:::align{center}

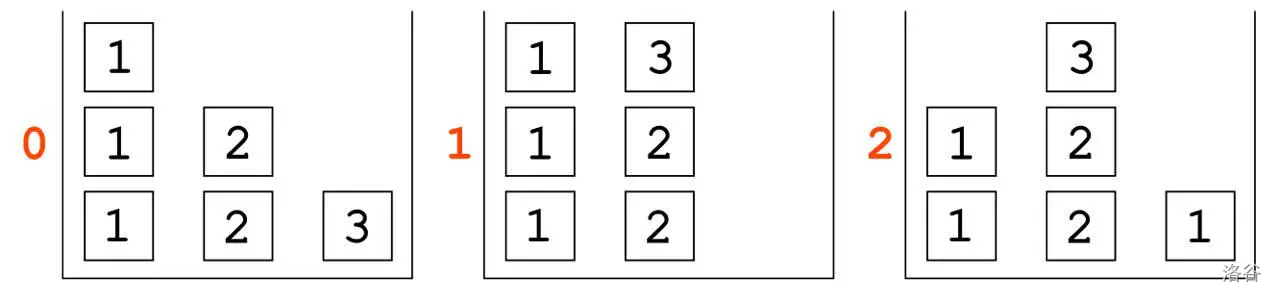First 3 states :::

After we have placed $1$, we need to place $2$ and $3$ in their places in the third column, again the only way to do this is to first move $3$ to the first column, because otherwise we will not be able to place $2$ in the third column in the next move, and then place $3$ in its place.

:::align{center}

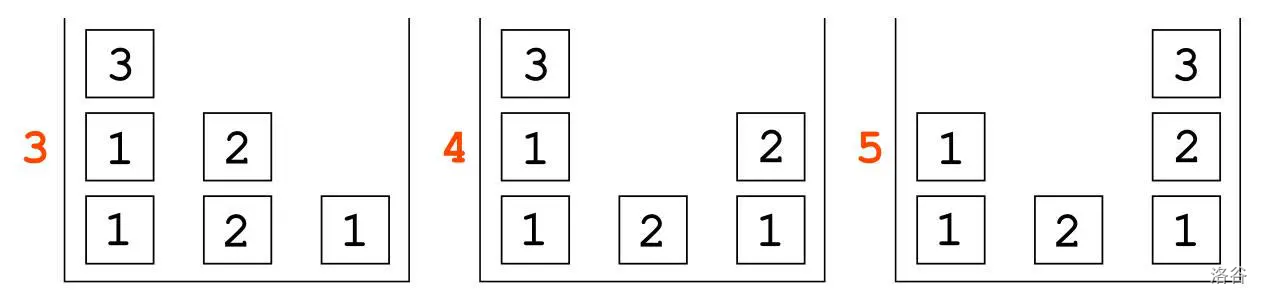
Next 3 states :::

After this, we want to correctly place the second column, and for $1$ to be the first number, we first need to take $2$, which we can only take in the last column. After we have placed $1$, we only need to return $2$ to the second column to achieve the desired state of the cubes.

:::align{center}

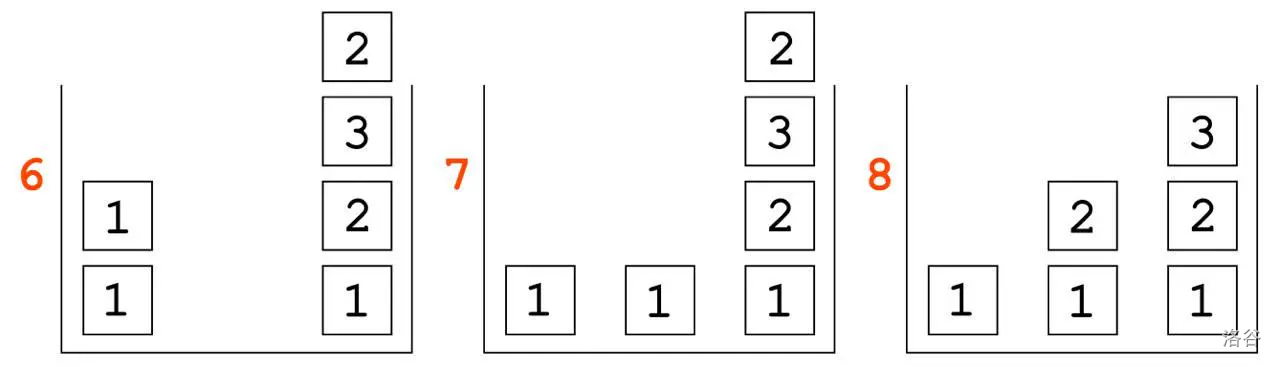
Final 3 states :::

Scoring

• ($12$ points): $n = 4$;
• ($20$ points): $n = 5$;
• ($20$ points): $n = 6$;
• ($20$ points): $n \le 10$;
• ($20$ points): $n \le 100$;
• ($8$ points): no additional restrictions.

You can earn half the points for each block if you output the correct $k$ for each test in the block. You will also receive a quarter of the points if you output an incorrect $k$, but the instructions are correct; in this case, $k \le 10^6$.

Note that to earn half the points, you need to output the correct $k$ and

• either output nothing else; that is, output only $k$, but no instructions;
• or output all $k$ instructions completely, where all column numbers are from $1$ to $n$. There are no additional requirements for them.

If you output, for example, only a few instructions, or too many instructions, or numbers that are not column numbers, etc., you will receive $0$ points.