题目描述

In the country of Trilyandia, there are $n$ cities connected by $n-1$ roads. The road system in this country is special:

• one road connects only two different cities;
• there can be at most one road between any two cities;
• from any city, it is possible to reach any other city, possibly passing through others.

The postal company OldPost decided to provide delivery services in this country. Due to the limited number of staff, transportation is carried out only along one route $a$ of length $l$, that is, a sequence of cities $a_1,a_2,\dots,a_l$ such that

• $a_i\neq a_j$ for ($i\neq j$);
• cities $a_i$ and $a_{i+1}$ are connected by a road $(1\leq i < l)$.

To maximize profit, OldPost decided to operate along the route with the maximum length.

An ancient competitor of OldPost --- NewPost decided to do the same, but along its own route $b$: $b_1,b_2,\dots,b_l$, which does not necessarily differ from $a$, but also has the maximum possible length.

The president, upon learning about the intentions of both companies, asked OldPost and NewPost to choose routes $a$ and $b$ in such a way as to cover the maximum number of cities (that is, to ensure that the maximum number of cities are in at least one route). Since the president of Trilyandia specializes in management, while the postal companies specialize in delivering items rather than finding routes, you have been tasked with finding such $a$ and $b$.

Note that each company wants to have the maximum possible length of its route; even if choosing a shorter route increases the total number of cities covered.

Help find routes $a$ and $b$ that have the maximum possible length and cover the maximum number of cities.

输入格式

The first line contains a single integer $n$ $(2\leq n \leq 6\cdot 10^5)$ --- the number of cities in the country.

Each of the next $n-1$ lines contains two integers $x_i$ and $y_i$ $(1 \leq x_i,y_i \leq n, x_i \neq y_i)$ --- pairs of cities between which there is a road.

输出格式

The first line should contain a single integer $l$ ($2 \leq l \leq n$) --- the length of the found trade routes.

The second line should contain $l$ integers $a_1,a_2,\dots,a_l$ ($1 \leq a_i \leq n$) --- the cities in route $a$.

The third line should contain $l$ integers $b_1,b_2,\dots,b_l$ ($1 \leq b_i \leq n$) --- the cities in route $b$.

If there are multiple optimal routes, output any of them.

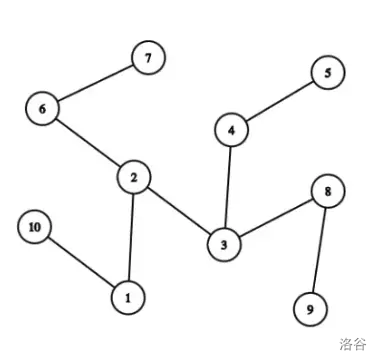
10
1 2
2 3
3 4
4 5
2 6
6 7
3 8
8 9
10 1

6
5 4 3 2 1 10 
9 8 3 2 6 7 

提示

:::align{center} :::

In the example, the longest possible routes are as follows:

• $5$-$4$-$3$-$2$-$6$-$7$
• $9$-$8$-$3$-$2$-$6$-$7$
• $5$-$4$-$3$-$2$-$1$-$10$
• $9$-$8$-$3$-$2$-$1$-$10$

The first and fourth routes allow covering all cities.

Scoring

• ($8$ points): $n\leq 10$;
• ($8$ points): $n\leq 20$;
• ($6$ points): $n \leq 1\,000$; there is exactly one city that is directly connected to all others;
• ($8$ points): $n \leq 20\,000$; there are exactly two cities that are connected to only one other city (the cities form a line);
• ($8$ points): $n \leq 20\,000$; there is exactly one city that is connected to three or more cities;
• ($8$ points): $n \leq 10\,000$; there are no more than $10$ cities that are connected to only one other city;
• ($16$ points): $n\leq 1\,000$;
• ($18$ points): $n\leq 70\,000$;
• ($20$ points): no additional restrictions.