题目描述

Consider two opaque planes $z = z_1$ and $z = z_2$ ($z_1 < z_2$) in a three-dimensional Cartesian coordinate system. Each plane has a convex polygonal hole, denoted as $P_1$ and $P_2$ respectively, which allows light to pass through.

There is a point light source $L$ moving in the plane $z = z_0$ ($z_2 < z_0$), in a direction parallel to the $xOy$ plane. The light source starts at the initial position $(x_0, y_0, z_0)$ at time $t = 0$ and moves with a constant velocity $\boldsymbol{v} = (v_x, v_y, 0)$. Therefore, at any time $t$, the position of the light source is given by $(x_0 + v_x t, y_0 + v_y t, z_0)$.

For a point $A$ in the plane $z = 0$, define it as $\textbf{illuminated}$ at time $t$ if and only if the segment $LA$ intersects the interiors (including boundaries) of both polygons $P_1$ and $P_2$. The $\textbf{illuminated area}$ at time $t$, denoted as $f(t)$, is the area formed by all illuminated points in the plane $z = 0$.

Define the $\textbf{average illuminated area}$ over the time period $[t_1, t_2]$, denoted as $\mathbb{E}[f(t) | t \sim U(t_1,t_2)]$, as the expected value of $f(t)$ over the interval $[t_1, t_2]$, assuming $t$ is a uniformly distributed random variable over $[t_1, t_2]$.

Given multiple time periods $[t_1, t_2]$, your task is to find the average illuminated area for each of these periods.

输入格式

The first line contains a single integer $T$ ($1\le T\le 10^4$) indicating the number of test cases.

For each test case, the first line contains five integers $x_0$, $y_0$, $z_0$, $v_x$, $v_y$ ($-10^5 \le x_0, y_0 \le 10^5$, $1 \le z_0 \le 10^5$, $-10^3 \le v_x, v_y \le 10^3$), representing the initial position of the light source $(x_0, y_0, z_0)$ and its velocity vector $\boldsymbol{v} = (v_x, v_y, 0)$. It is guaranteed that $\boldsymbol{v} \neq (0, 0, 0)$.

The second line contains two integers $n_1$ and $z_1$ ($3 \le n_1 \le 10^5$, $1 \le z_1 \le 10^5$), indicating the number of vertices of polygon $P_1$ and the value of $z_1$. Each of the following $n_1$ lines contains two integers $x_i$ and $y_i$ ($-10^5 \le x_i, y_i \le 10^5$), describing the vertices of $P_1$ in counterclockwise order.

The following line contains two integers $n_2$ and $z_2$ ($3 \le n_2 \le 10^5$, $1 \le z_2 \le 10^5$), indicating the number of vertices of polygon $P_2$ and the value of $z_2$. Each of the following $n_2$ lines contains two integers $x_j$ and $y_j$ ($-10^5 \le x_j, y_j \le 10^5$), describing the vertices of polygon $P_2$ in counterclockwise order.

It is guaranteed that no three or more vertices are collinear for $P_1$ and $P_2$.

The following line contains an integer $q$ ($1 \le q \le 10^5$), indicating the number of queries. Each of the following $q$ lines contains two integers $t_1$ and $t_2$ ($0 \le t_1 \le t_2 \le 10^3$), representing a time period.

It is guaranteed that the sum of $n_1+n_2$ and the sum of $q$ over all test cases do not exceed $10^5$, respectively, and $z_1 < z_2 < z_0$.

输出格式

For each query, output a real number representing the average illuminated area. Your answer will be considered correct only if the relative or absolute error between your answer and the correct answer does not exceed $10^{-4}$.

1
0 0 3 0 -1
4 1
1 0
3 0
3 2
1 2
4 2
0 0
1 0
1 1
0 1
3
0 10
1 2
1 1

0.450000000
1.125000000
2.250000000

提示

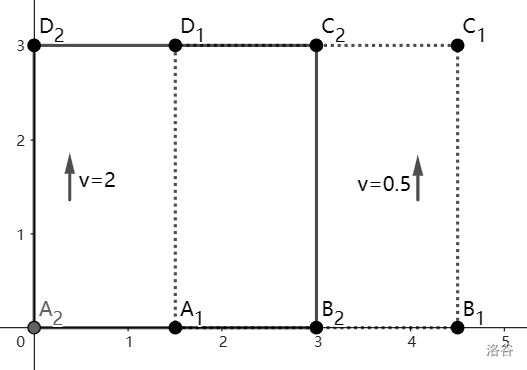
For the example, the projections of convex polygons $P_1$ and $P_2$ onto the $xOy$ plane at $t=0$, and the movement of these projections, are illustrated below. Polygon $A_1B_1C_1D_1$ is the projection of polygon $P_1$, and polygon $A_2B_2C_2D_2$ is the projection of polygon $P_2$.

:::align{center} :::