题目描述

哥萨克胡子来到铁路上，准备去测试魔法鞋，却发现整条铁路线上都有照明问题。铁路呈一个大“8”字形，火车在其上行驶。两条线路相交的地方称为交叉点。

:::align{center} :::

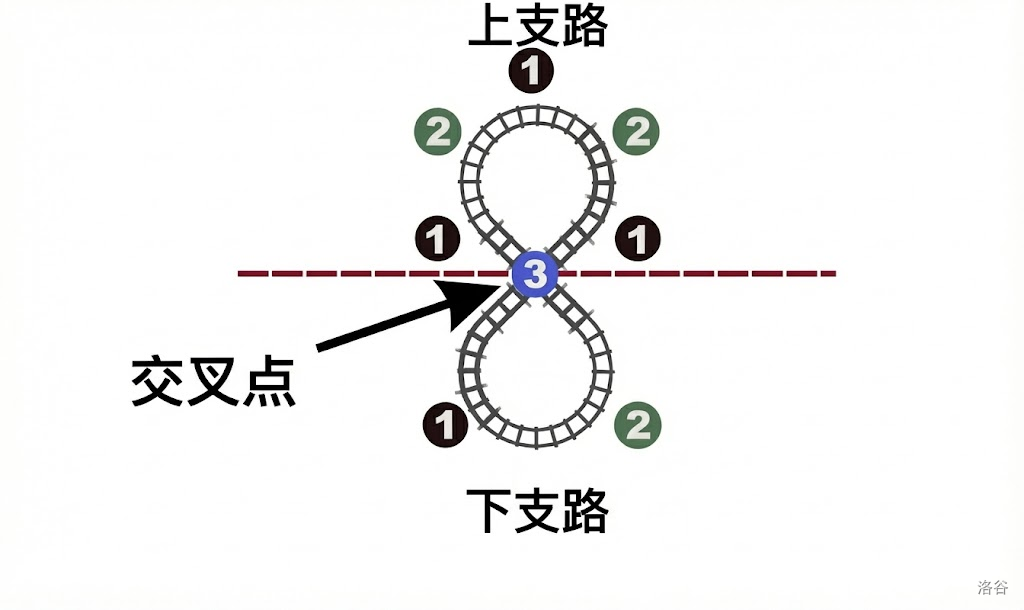哥萨克胡子想解决照明问题。为此，他购买了 $n$ 盏路灯，每盏灯的颜色为 $1$ 到 $k$ 中的一种。保证至少购买了每种颜色的一盏灯。当满足以下条件时，照明问题将被解决：

• 沿铁路线放置 $n$ 盏路灯。
• 其中一盏路灯位于交叉点上。
• 如果两盏路灯相邻（即它们位于同一条支线上，且它们之间没有其他路灯），则它们的颜色必须不同。
• 在铁路的上支路和下支路上（不包括交叉点）均至少有 $2$ 盏路灯。

请帮助哥萨克胡子找到任意一种解决照明问题的方法，或者指出该方法不存在。

输入格式

第一行包含三个整数 $n$、$k$ 和 $g$ ($5 \leq n \leq 2 \cdot 10^5$, $1 \leq k \leq 2 \cdot 10^5$, $0 \leq g \leq 8$) —— 分别表示路灯的数量、颜色的数量以及子任务编号。

下一行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$ ($1 \leq a_i \leq k$) —— 路灯的颜色。

保证从 $1$ 到 $k$ 的每个数字都在该数组中至少出现一次。

输出格式

如果无解，则输出 $-1$。

否则，在第一行输出两个数字 $x$ 和 $y$ ($2 \leq x, y < n$, $1 + x + y = n$) —— 分别表示上支路和下支路上（不包括交叉点）的路灯数量。

在第二行输出 $x$ 个数字 $b_1, b_2, \dots, b_x$ ($1 \leq b_i \leq k$) —— 上支路上路灯的颜色，按顺时针方向从交叉点后的第一个路灯开始排序。

在第三行输出一个数字 $c$ ($1 \leq c \leq k$) —— 位于交叉点的路灯颜色。

在第四行输出 $y$ 个数字 $d_1, d_2, \dots, d_y$ ($1 \leq d_i \leq k$) —— 下支路上路灯的颜色，按顺时针方向从交叉点后的第一个路灯开始排序。

如果存在多个答案，可以输出任意一个。

5 3 0
1 2 3 2 1

2 2
2 1 
3
1 2

8 3 0
1 1 1 1 2 2 2 3

5 2
1 2 1 2 1
3
2 1

7 3 0
1 1 1 1 1 2 3

-1

9 2 0
1 1 1 1 1 2 2 2 2

5 3
1 2 1 2 1 
2
1 2 1

6 6 0
1 2 3 4 5 6

3 2
6 2 5 
1
4 3

提示

样例说明

请注意，位于交叉点的路灯同时属于两条支路。

在第一个样例中，我们可以将颜色为 $1$ 和 $2$ 的两盏路灯放在上支路，将颜色为 $1$ 和 $2$ 的两盏路灯放在下支路，并将一盏颜色为 $3$ 的路灯放在交叉点。这样，每两盏相邻的路灯颜色都不同。

第二个样例对应于上图。

在第三个样例中，哥萨克胡子将无法解决照明问题，因为无论怎样放置，总会找到两盏相邻的颜色为 $1$ 的路灯。

评分细则

• （8 分）： $n \leq 8$。
• （20 分）： $n$ 为偶数，有一种颜色恰好出现 $\frac{n}{2}$ 次，且 $n \leq 1000$。
• （5 分）： $n = k$, $n \leq 1000$。
• （8 分）： $n \leq 18$; $k = 2$。
• （10 分）： $k = 2$, $n \leq 1000$。
• （14 分）： $k \neq 2$, $n \leq 1000$。
• （20 分）： $n \leq 1000$。
• （15 分）： 无额外限制。

翻译由 DeepSeek V3 完成