题目描述

flow 有一棵 $n$ 个点的有根树 $T$，根为 $1$，节点编号为 $1$ 至 $n$ 的正整数。

flow 想要构造一个新的有根树序列 $T_0=T,T_1,T_2,\dots$，满足 $T_{i+1}=f(T_i)$，对于所有 $i\ge 0$ 成立。

其中函数 $f(T)$ 定义如下（如有不理解，建议查看样例解释）：

1. 定义一棵树 $T'$。
2. 对 $T$ 做树链剖分（重链剖分），若存在多个儿子子树大小相等则取儿子编号较小的为重儿子。
3. 设第 $2$ 步中所有重链为 $L_1,L_2,\dots,L_k$，则 $T'$ 中的所有点编号为 $\{u\} = \{\min\limits_{v_1\in L_1}v_1,\min\limits_{v_2\in L_2}v_2,\dots,\min\limits_{v_k\in L_k}v_k\}$，可以证明，$L_i$ 的顺序不会改变最终 $T'$ 的结构。
4. 若对于 $i\ne j, \exist x\in L_i,y\in L_j$，且 $T$ 中存在一条边 $(x,y)$，则 $T'$ 中存在一条边 $(u_i,u_j)$，可以发现这样操作后 $T'$ 一定为一棵 $k$ 个结点的树。
5. 将 $T'$ 的根钦定为 $1$（注意到一定存在一个 $i$ 使得 $u_i=1$），返回 $T'$。

flow 给定了你 $T$，flow 想让你求出一个最小的 $m$，使得 $\forall m'\ge m,T_{m'}=T_m$，可以证明，在本题范围内，$m\le10^9$。

输入格式

第一行一个整数 $n$。

第二行 $n-1$ 个整数 $fa_2,fa_3,\dots,fa_n$，表示在以 $1$ 为根的情况下，$2\sim n$ 的父亲节点。

输出格式

一行一个整数，表示 $m$。

1

0

8
1 1 3 2 2 3 1

4

提示

样例 2 解释

一开始的 $T_0$ 为：

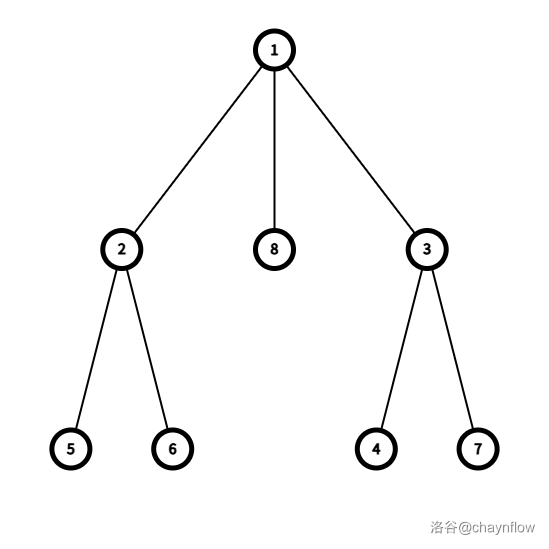
考虑 $f(T_0)$ 的过程：

1. $k=5,L_1=\{1,2,5\},L_2=\{6\},L_3=\{8\},L_4=\{3,4\},L_5=\{7\}$，注意 $L_i$ 的顺序其实不重要。
2. $T'$ 中的点： $\{u\}=\{1,6,8,3,7\}$。
3. $T'$ 中的边：$\{(1,3),(1,6),(1,8),(3,7)\}$。

• 故 $T_1=f(T_0)$ 为：

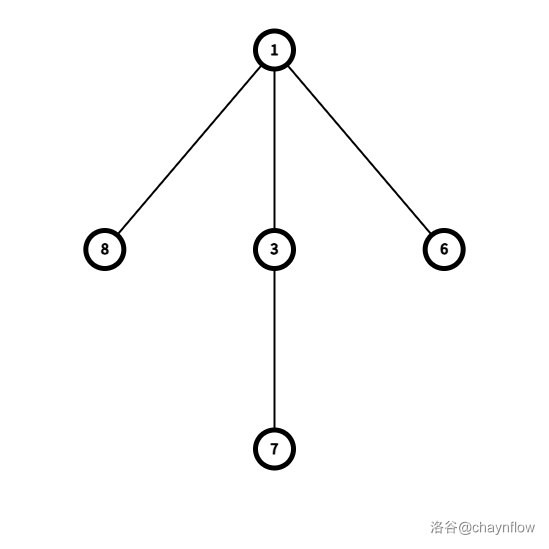
• 同理可得，$T_2=f(T_1)$ 为：

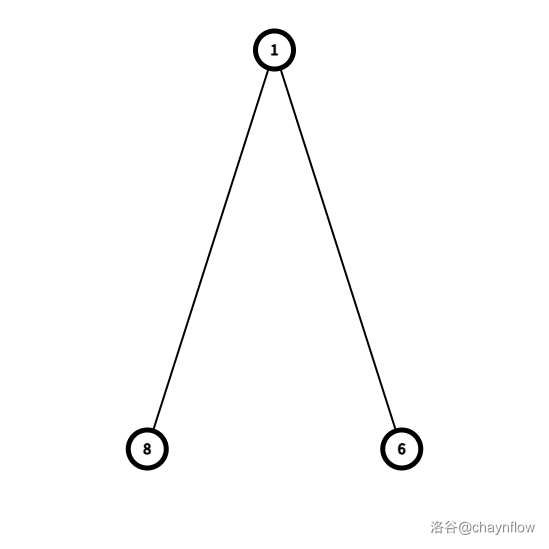
• $T_3=f(T_2)$ 为：

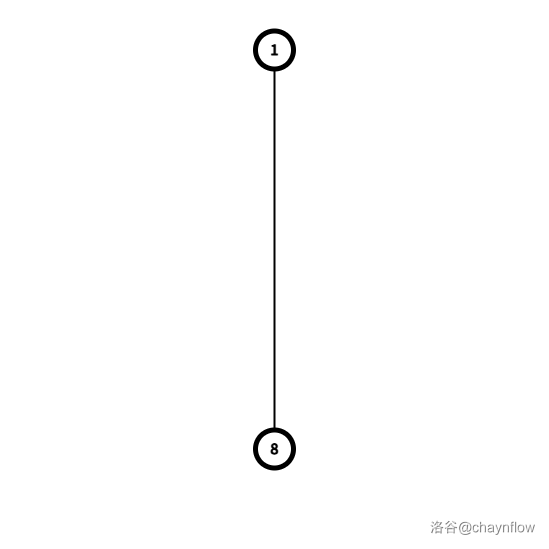
• $T_4=f(T_3)$ 为：

• $T_5=f(T_4)$ 为：

• $T_6=f(T_5)$ 为······

注意到对于 $m'\ge 4$，$T_{m'}=T_4$，故最终 $m=4$。

数据范围

请注意常数因子对程序运行效率带来的影响。

对于 $100\%$ 的数据，$1\le n\le 5\times10^6$，$1\le fa_i<i$。

• Subtask1(10pts)：$n\le5000$。
• Subtask2(5pts)：$T$ 的深度不超过 $2$（根节点的深度记为 $1$），$n\le10^5$。
• Subtask3(15pts)：$T$ 的深度不超过 $3$，$n\le10^5$。
• Subtask4(20pts)：$n\le10^5$。
• Subtask5(15pts)：$n\le5\times10^5$。
• Subtask6(35pts)：无特殊限制。