题目描述

给定一棵以 $1$ 为根结点的有根树 $T$，儿子之间有左右顺序。初始时，$T$ 只有一个结点 $1$。

接下来有 $n$ 次操作，第 $i$ 次操作给出 $f_i$，你需要新建一个结点 $i+1$ 作为 $f_i$ 最右侧的儿子结点，加入树 $T$。每次操作后，你需要回答以下问题：

对一棵树，定义「Trink 变换」为：

• 同时考虑所有不为 $1$ 的结点 $u$，如果 $u$ 不是 $u$ 父亲从左向右的第一个儿子，则把 $u$ 的父亲改为所有在 $u$ 左侧的兄弟中最靠右的一个。

问：对 $T$ 最少执行多少次 Trink 变换后，树 $T$ 满足，对树 $T$ 继续进行一次 Trink 变换后，树 $T$ 的形态保持不变。

询问之间互相独立。也就是说，并不会真的对原树进行「Trink 变换」。

输入格式

第一行，一个整数 $n$（$1 \leq n \leq 10^6$）。

第二行，$n$ 个整数，依次表示 $f_1, \ldots, f_n$（$1 \leq f_i \leq i$）。

输出格式

输出 $n$ 行，第 $i$ 行包含一个整数，表示第 $i$ 次操作后的答案。

5
1 1 2 2 5

0
1
2
3
4

提示

样例解释

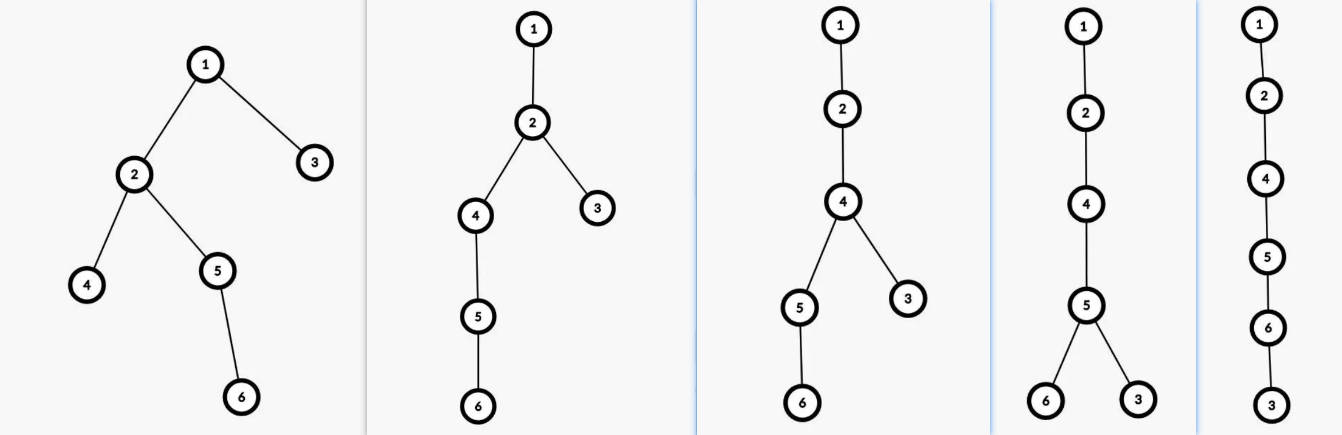
对于最后一次询问，以下展示了第 $k\ (0 \leq k \leq 4)$ 次操作后，树 $T$ 的形态：