题目描述

:::align{center} :::

She came up with a new jewelry design. The design uses two parts: a hollow circlet and a convex polygonal component. The design can be customized by specifying the edge lengths of the polygon, which should be multiples of a unit length, so that customers can embed memorial numbers in the jewelry. Note that there can be many different polygons with edges of the specified lengths. Among them, one with a circumscribed circle, that is, a circle that passes through all of its vertices, is chosen so that the polygonal component can be firmly anchored to the circlet.

:::align{center}

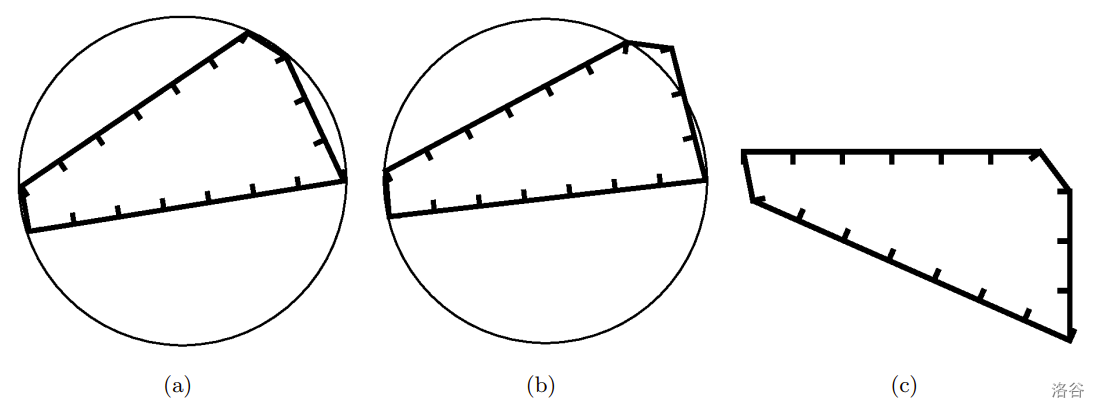
Figure E.2. (a) A pentagon with a circumscribed circle; (b) A pentagon with no circumscribed circle; (c) Another pentagon with no circumscribed circle :::

For example, Figure E.2(a) has a pentagon with its edge lengths of 3, 1, 6, 1, and 7 units, meaning March 16th and 17th. The radius of the circle is approximately 3.544 units. Figures E.2(b) and E.2(c) show pentagons with the same edge lengths but neither of them has a circumscribed circle.

To commercialize the jewelry, she needs to be able to compute the radius of the circumscribed circle from specified edge lengths. Can you help her by writing a program for this task?

输入格式

The input consists of a single test case of the following format.

$$\begin{aligned} &n\\ &x_1 \cdots x_n\\ \end{aligned}$$

$n$ is an integer that indicates the number of edges ($3 \le n \le 1000$). $x_k$ ($k = 1, \dots, n$) is an integer that indicates the length of the $k$-th edge ($1 \le x_k \le 6000$).

You may assume the existence of one or more polygons with the specified edge lengths. You can prove that one of such polygons has a circumscribed circle.

输出格式

Output the minimum radius of a circumscribed circle of a polygon with the specified edge lengths. Absolute/relative error of the output should be within $10^{-7}$.

5
3 1 6 1 7

3.54440435

3
500 300 400

250.0

6
2000 3000 4000 2000 3000 4000

3037.33679126

10
602 67 67 67 67 67 67 67 67 67

3003.13981697

3
6000 6000 1

3000.00001042