题目描述

A cross-shaped infinite area on the $x-y$ plane can be specified by two distinct points as depicted on the figure below.

:::align{center}

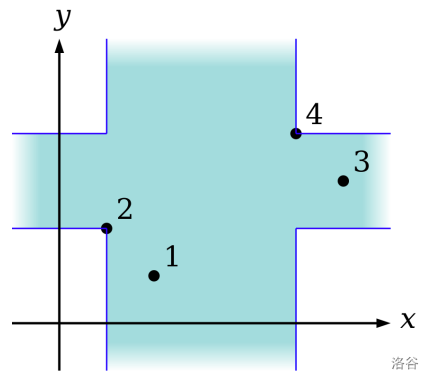
Figure J.1. The cross area specified by two points numbered 2 and 4 :::

Given a set of points on the plane, you are asked to figure out how many pairs of the points form a cross-shaped area that covers all the points. To be more precise, when $n$ points with coordinates $(x_i, y_i)$ ($i = 1, \dots, n$) are given, the ordered pair $\langle p, q \rangle$ is said to cover a point $(x, y)$ if $x_p \leq x \leq x_q$, $y_p \leq y \leq y_q$, or both hold. Your task is to find how many pairs $\langle p, q \rangle$ cover all the $n$ points. No two given points have the same $x$-coordinate nor the same $y$-coordinate.

输入格式

The input consists of a single test case of the following format.

$$\begin{aligned} &n \\ &x_1\ y_1 \\ &\vdots \\ &x_n\ y_n \end{aligned}$$

The first line contains an integer $n$ ($2 \leq n \leq 2 \times 10^5$), which is the number of points given. Two integers $x_i$ and $y_i$ in the $i$-th line of the following $n$ lines are the coordinates of the $i$-th point ($1 \leq x_i \leq 10^6$, $1 \leq y_i \leq 10^6$). You may assume that $x_j \neq x_k$ and $y_j \neq y_k$ hold for all $j \neq k$.

输出格式

Print in a line the number of ordered pairs of points that satisfy the condition.

4
2 1
1 2
6 3
5 4

4

20
15 9
14 13
2 7
10 5
11 17
13 8
9 3
8 12
6 4
19 18
12 1
3 2
5 10
18 11
4 19
20 16
16 15
1 14
7 6
17 20

9

提示

Figure J.1 depicts the cross specified by two points numbered 2 and 4, that are the second and the fourth points of the Sample Input 1. This is one of the crosses covering all the points.

Amendment

The conditions $x_p \leq x_q$, and $y_p \leq y_q$, have to be added to be satisfied for the ordered pair $\langle p, q \rangle$ that are counted. This was announced during the contest.