题目描述

If you talk about an even division in the usual sense of the words, it means dividing a thing equally. Today, you need to think about something different. A graph is to be divided into subgraphs with their numbers of nodes being even, that is, multiples of two.

You are given an undirected connected graph with even number of nodes. The given graph is to be divided into its subgraphs so that all the subgraphs are connected and with even number of nodes, until no further such division is possible. Figure 1.1 illustrates an example. The original graph of 8 nodes is divided into subgraphs with 4, 2, and 2 nodes. All of them have even numbers of nodes.

:::align{center}

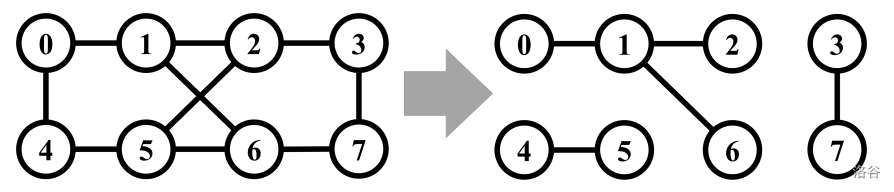
Figure I.1. Example of a division (Sample Input/Output 1) :::

To put it mathematically, an even division of a graph is the set of subsets $V_1, \dots, V_k$ of the graph nodes satisfying the following conditions.

1. $V_1 \cup \cdots \cup V_k$ is the set of all the nodes of the input graph, and $V_i \cap V_j = \emptyset$ if $i \neq j$.
2. Each $V_i$ is non-empty, and has an even number of elements.
3. Each $V_i$ induces a connected subgraph. In other words, any nodes in $V_i$ are reachable from each other by using only the edges of the input graph connecting two nodes in $V_i$.
4. There is no further division. For any $U_1 \cup U_2 = V_i$, the division obtained by replacing $V_i$ with the two sets, $U_1$ and $U_2$, does not satisfy either of the conditions 1, 2, or 3.

Your task is to find an even division of the given graph.

输入格式

The input consists of a single test case of the following format.

$$\begin{aligned} &n\ m \\ &x_1\ y_1 \\ &\vdots \\ &x_m\ y_m \end{aligned}$$

The first line consists of two integers $n$ and $m$. The first integer $n$ ($2 \leq n \leq 10^5$) is an even number representing the number of the nodes of the graph to be divided. The second integer $m$ ($n-1 \leq m \leq 10^5$) is the number of the edges of the graph.

The nodes of the graph are numbered from $0$ to $n-1$.

The subsequent $m$ lines represent the edges of the graph. A line $x_i\ y_i$ ($0 \leq x_i < y_i < n$) means that there is an edge connecting the two nodes $x_i$ and $y_i$. There are no duplicated edges. The input graph is guaranteed to be connected.

输出格式

If there exists an even division of the node set of the given graph into subsets $V_1, \dots, V_k$, print $k$ in the first line of the output. The next $k$ lines should describe the subsets $V_1, \dots, V_k$. The order of the subsets does not matter. The $i$-th of them should begin with the size of $V_i$, followed by the node numbers of the elements of $V_i$, separated by a space. The order of the node numbers does not matter either.

If there are multiple even divisions, any of them are acceptable.

8 9
0 1
1 2
2 3
0 4
1 6
3 7
4 5
5 6
6 7

3
2 3 7
2 4 5
4 0 1 2 6

2 1
0 1

1
2 0 1

提示

In the Sample 2, the singleton set of the set of the nodes of the original graph is already an even division.