题目描述

We are setting up a wireless communication network in a mountain range. Communication stations are to be located on the summits. The summits are on a straight line and have different altitudes.

To minimize the cost, our communication network should have a tree structure, which is a connected graph with the least number of edges. The structure of the network, that is, which stations to communicate with which other stations, should be decided in advance.

We construct the communication network as follows.

1. Initially, each station forms a tree consisting of only that station.
2. In each step, we merge two trees that are adjacent by making a link between two stations in different trees. Two trees are called adjacent when all the summits in between a summit in one tree and a summit in the other belong to one of these two trees. Stations to link are those on the highest summits of the two trees; they are uniquely determined because the altitudes of the summits are distinct.
3. Repeat the step 2 until all the stations are connected, directly or indirectly.

Figure D.1 depicts an example of the tree formation for Sample 1.

When a station detects an emergency event, an alert message should be broadcast to all the stations. On receiving a message, each station relays the message to all the stations with direct links, except for one from which it has come. The diameter of the network, that is, how many hops are sufficient to distribute messages initiated at any stations, depends on the choice of the two trees in the step 2 above.

To estimate the worst case delay of broadcast, we want to find the largest diameter of the network possibly constructed by the above procedure.

:::align{center}

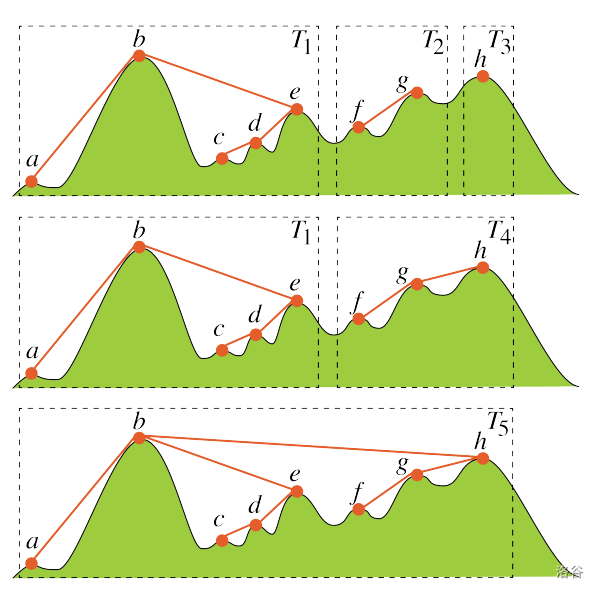
Figure D.1. The tree formation for Sample 1 :::

Obtained after some repetitions of step 2 with a certain series of choices. There are three trees, $T_1$, $T_2$, and $T_3$. Here, the station $h$ forms the tree $T_3$ consisting of only the station $h$.

Obtained by linking stations $g$ and $h$ in step 2. Trees $T_2$ and $T_3$, with top summits $g$ and $h$ respectively, are adjacent.

Obtained by linking stations $b$ and $h$ in the next step 2, merging two adjacent trees. Now all the stations form a single tree.

输入格式

The input consists of a single test case of the following format.

$$n$$ $$h_1$$ $$\vdots$$ $$h_n$$

Here, $n$ is the number of communication stations ($3 \leq n \leq 10^6$), and $h_i$ is an integer representing the altitude of the $i$-th station ($1 \leq h_i \leq n$). The altitudes of the stations are distinct, that is, $h_i \ne h_j$ if $i \ne j$.

输出格式

Output in a line a single integer representing the largest possible diameter of the tree.

8
1
8
2
3
5
4
6
7

6

4
1
2
3
4

3