题目描述

Let’s make sweets of a fancy shape that is a loop of chocolate.

:::align{center}

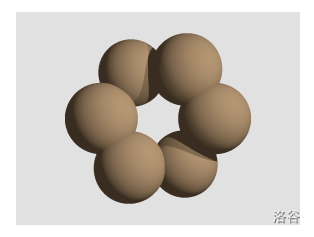
Figure A.1. A loop of chocolate formed by a union of six spheres :::

The shape of a loop is formed by a union of a number of spheres of the same size, where every sphere intersects with exactly two others.

:::align{center}

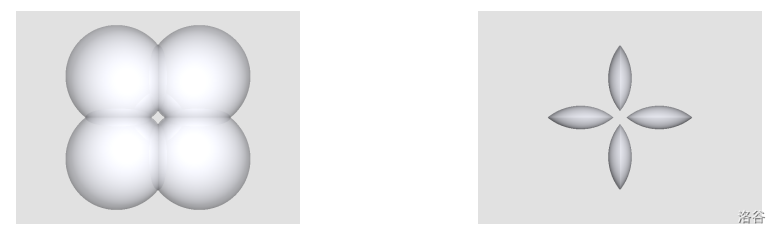
(a) Union of four spheres (b) Four intersections of the four spheres in (a)

Figure A.2. A loop of chocolate formed by a union of four spheres :::

Your job is to write a program that, for given the size and the positions of spheres, computes the total volume of the union of the spheres, i.e., the amount of chocolate required for filling the loop formed by the union.

[Hints] Two spheres of the same radius $r$ intersect each other when the distance between their centers, $d$, is less than $2r$. The volume of the intersection is known to be

$$\frac{2}{3}\pi(r - d/2)^2(2r + d/2).$$

The volume of the sphere of radius $r$ is $4\pi r^3/3$.

输入格式

The input consists of a single test case of the following format.

$$\begin{aligned} &n\ r \\ &x_1\ y_1\ z_1 \\ &\vdots \\ &x_n\ y_n\ z_n \end{aligned}$$

$n$ and $r$ are integers. $n$ is the number of spheres ($4 \leq n \leq 100$). All the spheres have the same radius $r$ ($2 \leq r \leq 100$). $(x_k, y_k, z_k)$ indicates the coordinates of the center of the $k$-th sphere ($k = 1, \dots, n$). All of $x_k$, $y_k$, and $z_k$ are integers between $-100$ and $100$, inclusive.

The $k$-th and the $k+1$-th spheres intersect each other for $1 \leq k < n$. The 1-th and the $n$-th spheres also intersect. No other pairs of spheres intersect.

输出格式

Output in a line the volume of the union of the spheres. Relative error of the output should be within $10^{-7}$.

6 9
20 0 10
20 10 0
10 20 0
0 20 10
0 10 20
10 0 20

17149.528141

4 12
10 10 0
10 -10 0
-10 -10 0
-10 10 0

27813.56696

6 9
23 3 13
20 10 0
10 20 0
3 23 13
0 10 20
10 0 20

17470.837758

4 2
0 0 0
3 0 0
3 3 0
0 3 0

122.52211349

8 70
100 100 0
0 100 0
-100 100 0
-100 0 0
-100 -100 0
0 -100 0
100 -100 0
100 0 0

10220648.1