题目描述

You are a salesperson at one of the ports in an island. You have to visit all the ports of the island and then come back to the starting port. Because you cannot swim and are scared of the sea, you have to stay on the land during your journey.

The island is modeled as a polygon on a two-dimensional plane. The polygon is simple, that is, its vertices are distinct and no two edges intersect or touch, other than consecutive edges which touch at their common vertex. In addition, no two consecutive edges are collinear. Each port in the island is modeled as a point on the boundary of the polygon. Your route is modeled as a closed curve that does not go outside of the polygon.

In preparation for the journey, you would like to compute the minimum length of a route to visit all the ports and return to the starting port.

输入格式

The input consists of a single test case of the following format.

$$\begin{aligned} &n \ m \\ &x_1 \ y_1 \\ &\vdots \\ &x_n \ y_n \\ &x'_1 \ y'_1 \\ &\vdots \\ &x'_m \ y'_m \end{aligned}$$

The first line contains two integers $n$ and $m$, which satisfy $3 \leq n \leq 100$ and $2 \leq m \leq 100$. Here, $n$ is the number of vertices of the polygon modeling the island, and $m$ is the number of the ports in the island. Each of the next $n$ lines consists of two integers $x_i$ and $y_i$, which are the coordinates of the $i$-th vertex of the polygon, where $0 \leq x_i \leq 1000$ and $0 \leq y_i \leq 1000$. The vertices of the polygon are given in counterclockwise order. Each of the $m$ following lines consists of two integers $x'_j$ and $y'_j$, which are the coordinates of the $j$-th port. The route starts and ends at $(x'_1, y'_1)$. It is guaranteed that all the ports are on the boundary of the polygon and pairwise distinct.

输出格式

Output in a line the minimum length of a route to visit all the ports and return to the starting port. The relative error of the output must be within $10^{-6}$.

4 4
0 0
2 0
2 2
0 2
1 0
1 2
2 1
0 1

5.656854249492381

8 2
0 0
4 0
4 4
0 4
0 3
3 3
3 1
0 1
0 0
0 4

16.64911064067352

提示

These samples are depicted in the following figures. The shortest routes are depicted by the thick lines. The gray polygons represent the islands. The small disks represent the ports in the islands. Note that the route does not have to be simple, i.e., the route may intersect or overlap itself as in the second sample, in which the same path between the two ports is used twice.

:::align{center}

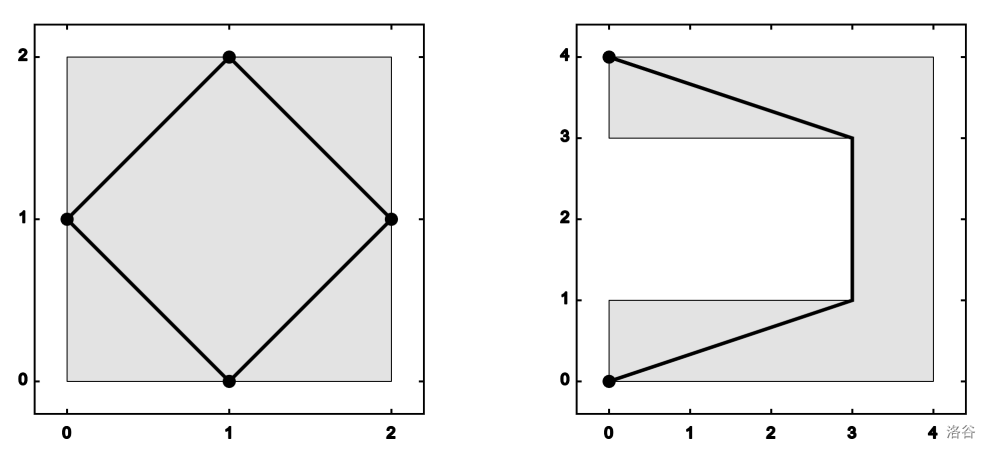
Figure J.1. Sample 1

Figure J.2. Sample 2 :::