题目描述

Some coins are placed on grid points on a two-dimensional plane. No two coins are stacked on the same point. Let’s call this placement of coins the source pattern. Another placement of the same number of coins, called the target pattern, is also given.

The source pattern does not match the target pattern, but by moving exactly one coin in the source pattern to an empty grid point, the resulting new pattern matches the target pattern. Your task is to find out such a coin move.

Here, two patterns are said to match if one pattern is obtained from the other by applying some number of 90-degree rotations on the plane and a parallel displacement if necessary, but without mirroring. For example, in the source pattern on the left of Figure D.1, by moving the coin at $(1,0)$ to $(3,1)$, we obtain the pattern on the right that matches the target pattern shown in Figure D.2.

:::align{center}

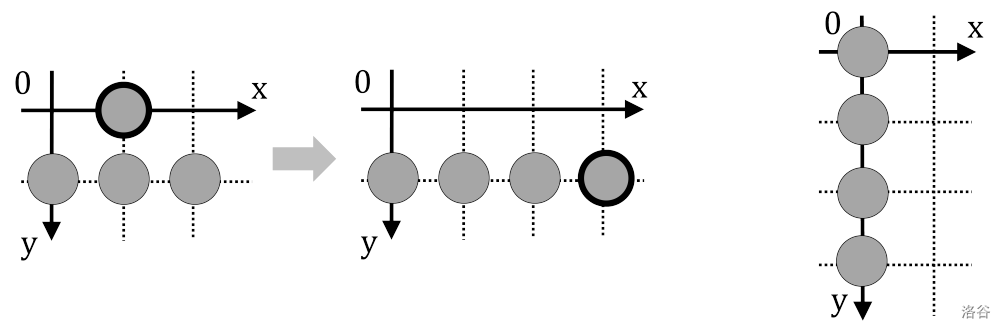
Figure D.1. Source pattern and a move

Figure D.2. Target Pattern :::

输入格式

The input consists of a single test case of the following format.

$$\begin{aligned} &h\ w \\ &p_{0,0} \cdots p_{0,w-1} \\ &\vdots \\ &p_{h-1,0} \cdots p_{h-1,w-1} \\ &H\ W \\ &P_{0,0} \cdots P_{0,W-1} \\ &\vdots \\ &P_{H-1,0} \cdots P_{H-1,W-1} \\ \end{aligned}$$

The first line consists of two integers $h$ and $w$, both between $1$ and $500$, inclusive. $h$ is the height and $w$ is the width of the source pattern description. The next $h$ lines each consisting of $w$ characters describe the source pattern. The character $p_{y,x}$ being 'o' means that a coin is placed at $(x,y)$, while 'x' means no coin is there.

The following lines with integers $H$ and $W$, and characters $P_{y,x}$ describe the target pattern in the same way.

输出格式

If the answer is to move the coin at $(x_0, y_0)$ to $(x_1, y_1)$, print $x_0$ and $y_0$ in this order separated by a space character in the first line, and print $x_1$ and $y_1$ in this order separated by a space character in the second line.

It is ensured there is at least one move that satisfies the requirement. When multiple solutions exist, print any one of them.

Note that $0 \leq x_0 < w$ and $0 \leq y_0 < h$ always hold but $x_1$ and/or $y_1$ can be out of these ranges.

2 3
xox
ooo
4 2
ox
ox
ox
ox

1 0
3 1

3 3
xox
oxo
xox
4 4
oxxx
xxox
xoxo
xxxx

1 2
-1 -1