题目描述

You are responsible for the security of ICPC (the Institute for Computer Program Critiques). The institute is in a one-storied building. Its rectangular floor is partitioned into square sections of the same size in a grid form. Two sections are said to be adjacent if they share an edge. Some of the sections in the building are blocked. All the sides of a blocked section are walled up and no entry is possible. All the other sections have no walls in between, and adjacent sections normally intercommunicate. However, roll-down shutters are equipped between some of the adjacent sections, so that closing such a shutter makes direct moves between the two sections impossible.

The top-secret research is being conducted in one of the outermost sections of the building. The section is called the top-secret section. The building has only one entrance at one of its outermost sections, which should be the only entry to the building. However, you have noticed that a window of one of the outermost sections is so fragile that it may allow trespassers to enter the building.

You must secure the top secret from trespassers. To do so, you may have to close some of the shutters so that breaking two or more closed shutters is required to make a route from the section with the fragile window to the top-secret section. In addition, there should exist at least one route from the entrance section to the top-secret section with no shutters closed on it.

You are to write a program that finds the minimum number of shutters to close to secure the top secret.

输入格式

The input consists of a single test case of the following format.

$$\begin{aligned} &n\ m \\ &s_1 \\ &\vdots \\ &s_n \\ &k \\ &r_1\ c_1\ d_1 \\ &\vdots \\ &r_k\ c_k\ d_k \\ \end{aligned}$$

$n$ and $m$ are integers between $2$ and $100$, inclusive, representing that the building floor has $n$ rows and $m$ columns of sections. The section in the $j$-th column of the $i$-th row is identified as section $(i,j)$. The $i$-th line of the following $n$ lines has a string $s_i$ of length $m$ describing the sections in the $i$-th row. Each character of $s_i$ is one of . , #, S, T, and U. If the $j$-th character of $s_i$ is #, section $(i,j)$ is blocked and is impassable; otherwise, the section is passable. The $j$-th character of $s_i$ being S means that section $(i,j)$ is the entrance section, T means the top-secret section, and U means the entry point of the trespassers, that is, the section with a fragile window. Each of S, T, and U occurs exactly once in the input as an outermost section. The top-secret section is reachable from the entrance through passable sections with no shutters closed.

$k$ is the number of the shutters in the building. The $i$-th line in the following $k$ lines describes a shutter by two integers $r_i$ and $c_i$, and a character $d_i$. $d_i$ is either r or b. If $d_i$ is r, $1 \leq r_i \leq n$ and $1 \leq c_i < m$ hold, and a shutter is equipped between sections $(r_i, c_i)$ and $(r_i, c_i + 1)$. If $d_i$ is b, $1 \leq r_i < n$ and $1 \leq c_i \leq m$ hold, and a shutter is equipped between sections $(r_i, c_i)$ and $(r_i + 1, c_i)$. The same combination of $r_i$, $c_i$, and $d

输出格式

Output a single integer in a line which is the minimum number of shutters to close to secure the top secret. If that is not possible, output $-1$. If trespassing to the top-secret section is not possible with all shutters open, output $0$.

3 3
S..
#..
U.T
7
1 2 b
1 3 b
2 2 b
2 2 r
2 3 b
3 1 r
3 2 r

3

2 2
ST
.U
4
1 1 r
1 1 b
1 2 b
2 1 r

-1

7 10
U.........
..........
###.......
..........
.......###
..........
S........T
18
4 4 r
5 4 r
6 7 r
7 7 r
3 4 b
3 5 b
3 6 b
3 7 b
3 8 b
3 9 b
3 10 b
5 1 b
5 2 b
5 3 b
5 4 b
5 5 b
5 6 b
5 7 b

14

提示

Sample Input 1 is depicted in the following figure. The dotted lines represent where the shutters are equipped.

:::align{center}

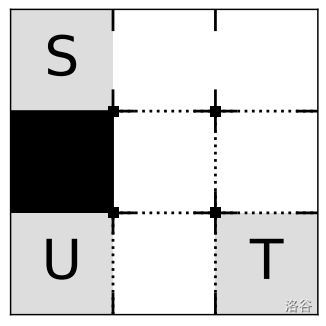
Figure C.1. Sample Input 1 :::