题目描述

You are the head of a group of $n$ employees including you in a company. Each employee has an employee ID, which is an integer 1 through $n$, where your ID is 1. Employees are often called by their IDs for short: $\#1$, $\#2$, and so on. Every employee other than you has a unique immediate boss, whose ID is smaller than his/hers. A boss of an employee is transitively defined as follows.

• If an employee $\#i$ is the immediate boss of an employee $\#j$, then $\#i$ is a boss of $\#j$.
• If $\#i$ is a boss of $\#j$ and $\#j$ is a boss of $\#k$, then $\#i$ is a boss of $\#k$.

Every employee including you is initially assigned exactly one task. That task can be done by him/herself or by any one of his/her bosses. Each employee can do an arbitrary number of tasks, but doing many tasks makes the employee too tired. Formally, each employee $\#i$ has an individual fatigability constant $f_i$, and if $\#i$ does $m$ tasks in total, then the fatigue level of $\#i$ will become $f_i \times m^2$.

Your mission is to minimize the sum of fatigue levels of all the $n$ employees.

输入格式

The input consists of a single test case in the following format.

$$\begin{aligned} & n \\ & b_2 \ b_3 \ \cdots \ b_n \\ & f_1 \ f_2 \ \cdots \ f_n \\ \end{aligned}$$

The integer $n$ in the first line is the number of employees, where $2 \leq n \leq 5 \times 10^5$. The second line has $n-1$ integers $b_i$ ($2 \leq i \leq n$), each of which represents the immediate boss of the employee $\#i$, where $1 \leq b_i < i$. The third line has $n$ integers $f_i$ ($1 \leq i \leq n$), each of which is the fatigability constant of the employee $\#i$, where $1 \leq f_i \leq 10^{12}$.

输出格式

Output the minimum possible sum of fatigue levels of all the $n$ employees.

4
1 1 2
1 1 1 1

4

4
1 1 2
1 10 10 10

16

4
1 1 2
1 2 4 8

10

提示

:::align{center}

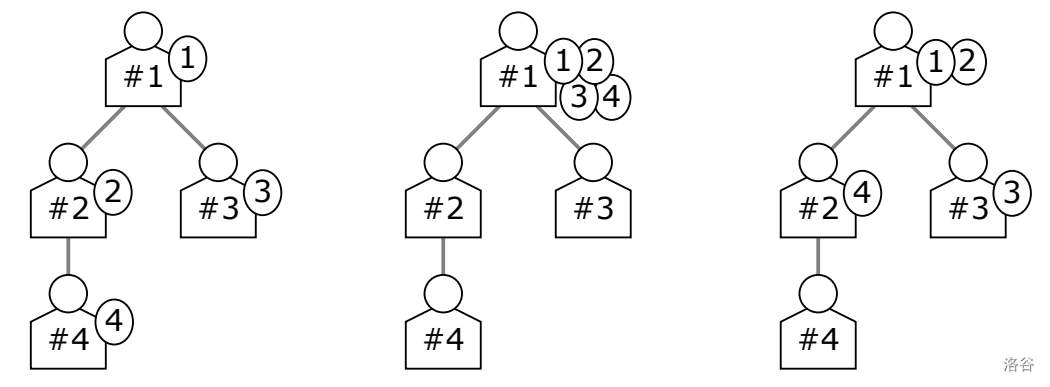
Figure J.1. Illustration of the three samples (from left to right) :::

The situations and solutions of the three samples are illustrated in Figure J.1.

For Sample Input 1, the unique optimal way is that each employee does his/her task by him/herself. That is, you should just say "Do it yourself!" to everyone.

For Sample Input 2, the unique optimal way is that the employee $\#1$ does all the tasks. That is, you should just say "Leave it to me!" to everyone.

For Sample Input 3, one of the optimal ways is the following.

• $\#1$ does the tasks of $\#1$ and $\#2$, and then the fatigue level of $\#1$ will be $1 \times 2^2 = 4$.
• $\#2$ does the task of $\#4$, and then the fatigue level of $\#2$ will be $2 \times 1^2 = 2$.
• $\#3$ does the initially assigned task, and then the fatigue level of $\#3$ will be $4 \times 1^2 = 4$.
• $\#4$ does nothing, and then the fatigue level of $\#4$ will be $8 \times 0^2 = 0$.

Thus, the sum of the fatigue levels is $4 + 2 + 4 + 0 = 10$. There is another optimal way, in which the employees $\#1$, $\#2$, and $\#3$ do their initially assigned tasks by themselves and $\#1$ does the task of $\#4$ in addition.