题目描述

Your fortune is to be told by a famous fortune teller. She has a number of tarot cards and a six-sided die. Using the die, she will choose one card as follows and that card shall tell your future.

Initially, the cards are lined up in a row from left to right. The die is thrown showing up one of the numbers from one through six with equal probability. When $x$ is the number the die shows up, the $x$-th card from the left and every sixth card following it, i.e., the $(x + 6k)$-th cards for $k = 0, 1, 2, \ldots$, are removed and then remaining cards are slid left to eliminate the gaps. Note that if the number of cards remaining is less than $x$, no cards are removed. This removing and sliding procedure is repeated until only one card remains.

Figure G.1 illustrates how cards are removed and slid when the die shows up two.

:::align{center}

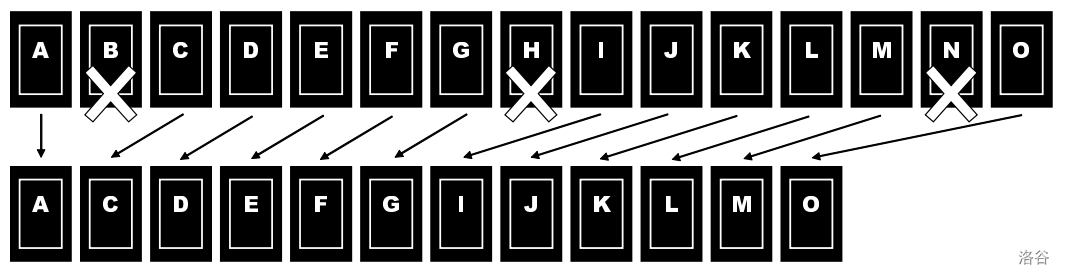
Figure G.1. Removing and sliding cards :::

You are given the number of initial tarot cards. For each card initially placed, compute the probability that the card will remain in the end.

输入格式

The input is a single line containing an integer $n$, indicating the number of tarot cards, which is between $2$ and $3 \times 10^5$, inclusive.

输出格式

Output $n$ lines, the $i$-th of which should be an integer that is determined, as follows, by the probability of the $i$-th card from the left to remain in the end.

3

332748118
332748118
332748118

7

305019108
876236710
876236710
876236710
876236710
876236710
305019108

8

64701023
112764640
160828257
160828257
160828257
160828257
112764640
64701023

提示

For Sample Input 1, the probabilities to remain in the end for all the cards are equal, that are $1/3$.

For Sample Input 2, let us consider the probability of the leftmost card to remain in the end. To make this happen, the first number the die shows up should not be one. After getting a number other than one, six cards will remain. Each of these six cards will remain in the end with the same probability. From this observation, the probability of the leftmost card to remain in the end is computed as $(5/6) \times (1/6) = 5/36$. The same argument holds for the rightmost card. As for the rest of the cards, the probabilities are equal, and they are $(1 - 2 \times 5/36)/5 = 13/90$.