题目描述

You are given a set of square cells arranged in a chessboard-like pattern with $n$ horizontal rows and $n$ vertical columns. Rows are numbered 1 through $n$ from top to bottom, and columns are also numbered 1 through $n$ from left to right.

Initially, the cells are colored as in a chessboard, that is, the cell in the row $i$ and the column $j$ is colored black if $i + j$ is odd and is colored white if it is even.

Color-inversion operations, each of which is one of the following two, are made one after another.

Invert colors of a row: Given a row number, invert colors of all the cells in the specified row. The white cells in the row become black and the black ones become white.

Invert colors of a column: Given a column number, invert colors of all the cells in the specified column. The white cells in the column become black and the black ones become white.

The number of distinct areas after each of the operations should be counted. Here, an area means a group of directly or indirectly connected cells of the same color. Two cells are said to be directly connected when they share an edge.

输入格式

The input consists of a single test case of the following format.

$$\begin{aligned} &n\ q \\ &operation_1 \\ &\vdots \\ &operation_q \end{aligned}$$

The integer $n$ is the number of rows and columns ($1 \leq n \leq 5 \times 10^5$). The integer $q$ is the number of operations ($1 \leq q \leq 5 \times 10^5$). The following $q$ lines represent operations to be made in this order. Each of them is given in either of the following forms.

• ROW $i$: the operation “invert colors of a row” applied to the row $i$ ($1 \leq i \leq n$).
• COLUMN $j$: the operation “invert colors of a column” applied to the column $j$ ($1 \leq j \leq n$).

输出格式

Output $q$ lines. The $k$-th line should contain an integer denoting the number of areas after the $k$-th operation is made.

3 3
ROW 2
COLUMN 3
ROW 2

3
2
6

200000 2
ROW 1
ROW 1

39999800000
40000000000

提示

:::align{center}

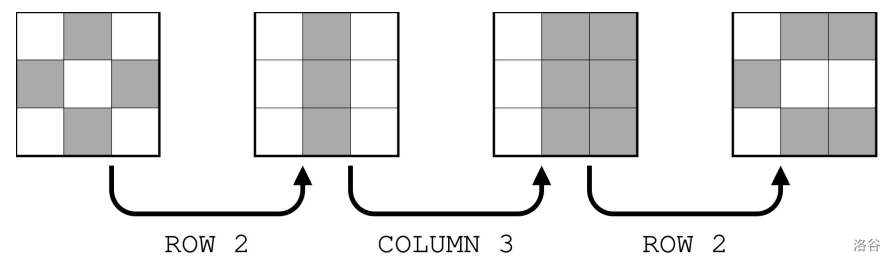
Figure F.1. Illustration of Sample Input 1 :::