题目描述

简单多边形是平面中由线段组成的闭合曲线，这些线段首尾相连，除了因连接共用的线段端点，任何两个线段都不能彼此相交。

简单多边形可以分为两类：凸多边形和凹多边形。一个凸多边形是指：多边形中任意两点间的线段上的所有点都在多边形内，包括在内部或边界上。不是凸多边形的简单多边形就是凹多边形。如下图，左边是一个凸多边形，右边是一个凹多边形。

:::align{center} :::

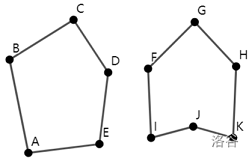现在，给定 $n$ 个点，满足所有点互不相同，且不存在三个点在同一条直线上。你的任务是选择这 $n$ 个点中的一些点（可以全选），并按照任意顺序依次连边，最后需要连成一个面积严格大于 $0$ 的 $\textbf{凹多边形}$。你需要求出能形成的凹多边形的面积最大是多少。

输入格式

第一行一个正整数 $T$ ($1\le T \le 10^4$)，表示数据组数。

对于每组数据，第一行一个正整数 $n$ ($3\le n \le 10^5$)，表示点数。

接下来 $n$ 行，每行两个整数 $x_i, y_i$ ($-10^9 \le x_i,y_i \le 10^9$)，表示各个点的坐标。保证所有点的坐标互不相同，且不存在三点共线。

各个测试数据组的 $n$ 之和不超过 $2\cdot 10^5$。

输出格式

对于每组数据，如果不能形成面积严格大于 $0$ 的凹多边形，输出 $-1$；否则，输出一个正整数，表示形成的最大的凹多边形的面积的两倍。可以证明这个答案是一个正整数。

2
6
-2 0
1 -2
5 2
0 4
1 2
3 1
4
0 0
1 0
0 1
1 1

40
-1