题目描述

There is a triangle whose coordinates of three vertices $A, B,$ and $C$ are all integers. If you select a point on each side of the triangle whose coordinates are integers and connect those points, a new triangle is created. When creating a new triangle, no vertex of the given triangle can be selected as a vertex of the new triangle.

Depending on which points you select and connect, the area of the newly created triangle may be large or small.

You are to write a program that finds out the largest and smallest areas of the newly created triangle if they exist.

For example, as shown in the figure below, if the coordinates of the three vertices of the given triangle are $(4,8)$, $(-8,-1)$, and $(7,-7)$, the yellow triangle shown in Fig. L.1(a) has the largest area among those that satisfy the condition, and the blue triangle shown in Fig. L.1(b) has the smallest area.

:::align{center} :::

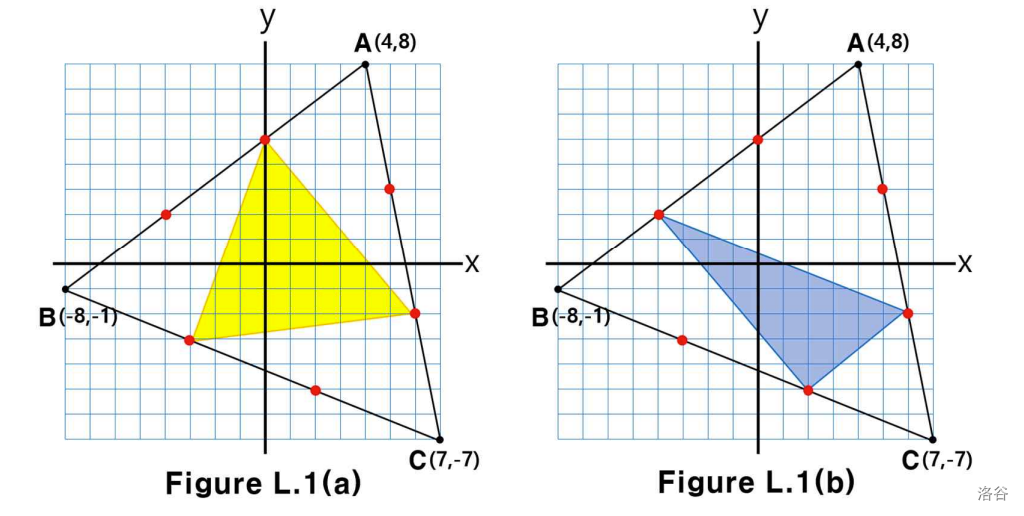There may not be a point on any side of the given triangle whose coordinates are integers, in which case the triangle you are looking for does not exist.

It is guaranteed that the three points of the given input are not on a straight line.

输入格式

Your program is to read from standard input. The input consists of a line containing six integers that are the $(x,y)$-coordinates of the three vertices $A = (A_x, A_y)$, $B = (B_x, B_y)$, and $C = (C_x, C_y)$ of a triangle, which $A_x$, $A_y$, $B_x$, $B_y$, $C_x$, and $C_y$ are given in that order. Each value of the coordinates is an integer between $-10^9$ and $10^9$, inclusive.

输出格式

Your program is to write to standard output. Let the area of the newly created triangle with the largest area be $S_{\text{max}}$, and the area of the triangle with the smallest area be $S_{\text{min}}$. If such triangles can be found, print $2S_{\text{max}}$ and $2S_{\text{min}}$ in that order, where both $2S_{\text{max}}$ and $2S_{\text{min}}$ are positive integers. If such triangles cannot be found, print $-1$.

4 8 -8 -1 7 -7

69 46

-8 1 7 11 7 -5

121 23

0 0 1 10 10 0

-1