题目描述

ICPC street is currently an undeveloped area, with a large-scale development plan scheduled soon. Before starting the development, information about $n$ important points along the street will be collected using $n$ remote-controlled robots, with each robot collecting information from one of these important points. Now, the goal is to combine all the collected information into a single robot to find the most efficient development approach. To combine the information, the robots can move towards left or right and combine the information that they have from other robots. Also, each robot is powered by its own battery, and all the robots are equipped with identical batteries. Specifically, let $p_1, p_2, \dots, p_n$ represent the positions of the important points where the robots collect information, arranged from left to right. Then the requirements are as follows:

1. The ICPC street is considered as a one-dimensional interval $[0, L]$ with a positive integer $L$. The important points $p_1, p_2, \dots, p_n$ are always represented as integers on the interval, including two endpoints of the interval. That is, $p_1 = 0$ and $p_n = L$. Initially, each robot is positioned at one of the important points, so it has the information of the important point before beginning to move. Note that there is exactly one robot at each of these points initially, which means $n$ is also the number of robots, and always at least 2 and at most $L+1$.

2. For combining the information from other robots, robots can move freely to the left or right, consuming 1 unit of battery for 1 unit of distance traveled, regardless of direction. All robots are equipped with the same battery capacity with integer $P$, and move only in integer units of distance.

3. When two or more robots meet at the integer position on the street, they can combine each other's information. For example, if a robot with information about $p_1$ and $p_2$ encounters with a robot with information about $p_3$ and $p_4$, both robots will then have information about the positions $p_1, p_2, p_3$, and $p_4$.

4. Robots consume the battery only for movement. Therefore, they do not use the battery when changing direction or when combining the information from other robots.

5. After all movements, at least one robot must have information about all the positions $p_1, p_2, \dots, p_n$.

:::align{center} :::

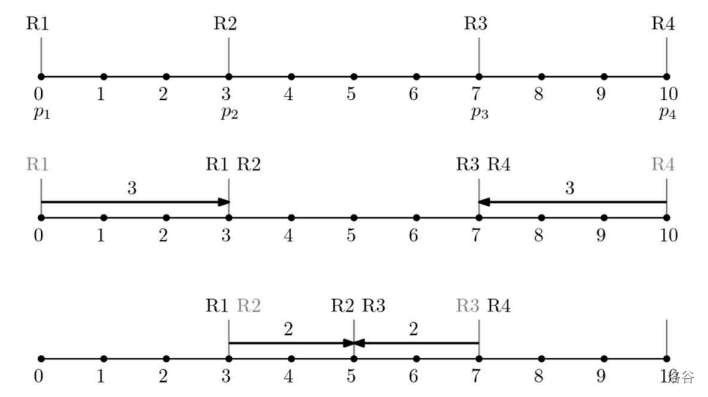For example, the figure above shows an example with $L=10$, $n=4$, and Robots 1, 2, 3, and 4 (R1, R2, R3, R4 in the figure) collect information (and are initially positioned) at $p_1=0$, $p_2=3$, $p_3=7$, and $p_4=10$, respectively. Then the following sequence of steps can be performed with a battery capacity of $P=3$:

1. Robot 1 moves to $p_2$, and Robots 1 and 2 combine each other's information.
2. Robot 4 moves to $p_3$, and Robots 3 and 4 combine each other's information.
3. Robot 2 moves 2 units to the right, Robot 3 moves 2 units to the left, and they combine each other's information at the position 5 on the street.

Then after completing the process, Robots 2 and 3 will have information about all the positions $p_1, p_2, p_3$, and $p_4$.

Since the battery is much more expensive than the other parts of robot, it is important to determine the minimum battery capacity required for each robot for efficient data collection. Given $L$, $n$, and the positions of the important points $p_1, p_2, \dots, p_n$, write a program to calculate the minimum battery capacity $P$ required for at least one robot to have information about all the important points.

输入格式

Your program is to read from standard input. The input starts with a line containing two positive integers, $L$ and $n$ ($1 \leq L \leq 10^6$, $2 \leq n \leq L+1$), where $n$ is the number of robots and important points on the street and $L$ is the position of the right endpoint of the street. In the following line, $n$ distinct integers between 0 and $L$ that represent the positions of important points of the street (the initial positions of the robots) are given in increasing order, where the first integer is 0 and the last one is $L$.

输出格式

Your program is to write to standard output. Print exactly one line. The line should contain a single integer that represents the minimum battery capacity $P$ required for at least one robot to have information about all the important points.

10 4
0 3 7 10

3

100 5
0 97 98 99 100

49

1 2
0 1

1