题目描述

There are $n$ bins arranged in a row and $2n$ balls on the ground. The balls are numbered from 1 to $n$ and there are exactly two balls numbered $i$, for each $i$, $1 \leq i \leq n$. Also, for $1 \leq i \leq n$, the $i$-th bin is denoted by $B_i$ and each bin $B_i$ can contain at most two balls. Initially, the bin $B_i$ contains both of ball $n+1-i$'s, for $1 \leq i \leq n$. See the Figure F.1 below for the initial configuration of bins.

:::align{center}

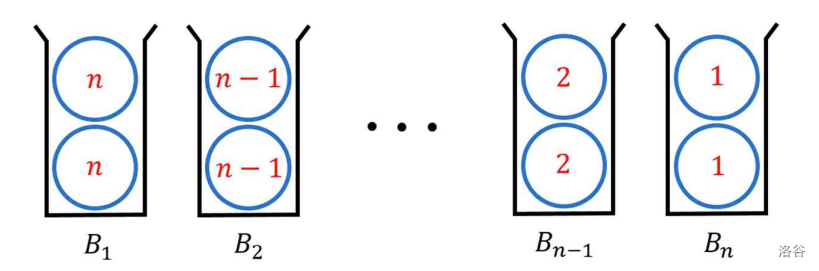
Figure F.1. The initial configuration of bins :::

You can swap two balls only from adjacent bins, which implies one swap operation. Note the bin is not a stack and for adjacent bins $B_i$ and $B_{i+1}$, you can swap the one of two balls in $B_i$ and the one in $B_{i+1}$. See the Figure F.2 below. The figure represents two swap operations.

:::align{center}

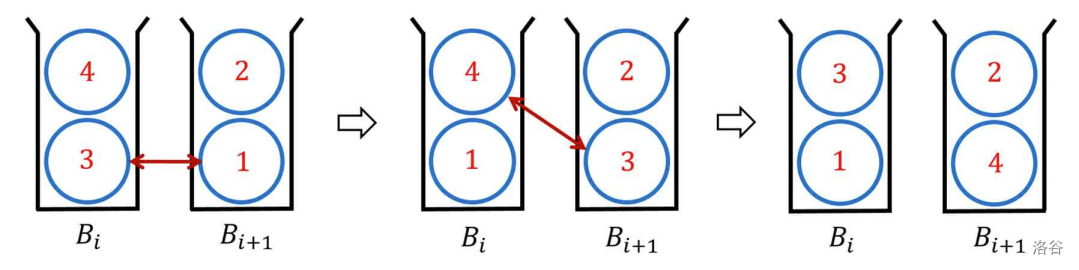
Figure F.2. The swap operations between adjacent bins :::

Through these swap operations, you should sort the balls. As a result of the sorting, the bin $B_i$ must contain the both of ball $i$'s, for $1 \leq i \leq n$. In particular, the total number of swap operations should be no more than $\text{Bound}$, when $\text{Bound}$ is given as a function of $n$, especially, $\text{Bound} = 0.7n^2$.

Given $n$ bins and $2n$ balls, write a program to find a sorting method of balls such that the total number of swap operations is no more than $\text{Bound} = 0.7n^2$.

输入格式

Your program is to read from standard input. The input consists of exactly one line. The line contains an integer $n$ ($3 \leq n \leq 100$), representing that there are $n$ bins and $2n$ balls.

输出格式

Your program is to write to standard output. Let $S$ be the total number of swap operations in your sorting method for the input. Print exactly $S+1$ lines. The first line contains $S$. Each of the following $S$ lines contains three integers $j, a,$ and $b$, representing one swap operation between the ball $a$ in the bin $B_j$ and the ball $b$ in $B_{j+1}$, where $1 \leq j \leq n-1$ and $1 \leq a, b \leq n$. The swap operations in your sorting method should be printed in order, one per line. The number $S$ must satisfy that $S \leq 0.7n^2$.

3

6
1 3 2
2 3 1
1 2 1
1 3 2
2 3 1
1 2 1

3

5
1 3 2
2 3 1
1 3 1
2 3 1
1 2 1