题目描述

The Mausoleum of King Geo III is a huge stone structure in the shape of a histogram. A histogram is a simple rectilinear polygon whose boundary consists of two chains: an upper chain that is monotone with respect to the horizontal axis, and a lower chain that is a horizontal line segment, called the base segment (see Figure E.1).

:::align{center} :::

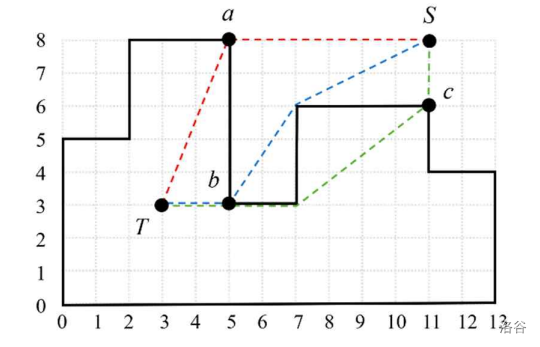
It is rumored that a hidden treasure lies somewhere within this mausoleum. Metry, a renowned treasure hunter, has uncovered the treasure's location at point $T$. Metry's plan is to break through the mausoleum's walls, enter, and retrieve the treasure. She will start at a specific location $S$ outside the mausoleum. Using her equipment, Metry can drill through only one point, which corresponds to a vertex on the boundary of the mausoleum. Since the time required to drill through the walls is the same at all vertices, the key to minimizing the time spent is to find the shortest path from $S$ to $T$.

Figure E.1 illustrates a mausoleum along with several possible paths from $S$ to $T$, where the vertices are pierced only once. The path through vertex $a$ has a total length of $11.385165 = 6 + \sqrt{29}$, the path through vertex $b$ has a length of $10.077687 = \sqrt{20} + \sqrt{13} + 2$, and the path through vertex $c$ has a length of $11.0 = 2 + \sqrt{25} + 4$. Among these, the shortest path is through vertex $b$.

Given the boundary of the mausoleum and the positions of $S$ and $T$, write a program to find the length of the shortest path from $S$ to $T$ with a single vertex piercing.

输入格式

Your program is to read from standard input. The input starts with a line containing an integer, $n$ ($4 \leq n \leq 100,000$), where $n$ is even and is the number of vertices of a histogram representing the mausoleum. In the second line, $n$ integers $v_1, v_2, \ldots, v_n$ ($v_1 = v_n = 0$, $0 \leq v_i \leq 10^6$) are given, which represent the x-coordinates of the vertical edges and the y-coordinates of the horizontal edges. The vertical and horizontal edges alternate as you traverse the upper chain of the histogram, from the left end to the right end of the base segment. The length of each edge is at least 1, and the x-coordinates are given in strictly increasing order. The last line contains four integers $s_x, s_y, t_x,$ and $t_y$ ($-10^6 \leq s_x, s_y \leq 2 \times 10^6$, $0 < t_x, t_y < 10^6$), where $(s_x, s_y)$ and $(t_x, t_y)$ correspond to the points $S$ and $T$, respectively. Notice that $S$ is a point outside the histogram and $T$ is a point inside the histogram, neither of which lies on the boundary.

输出格式

Your program is to write to standard output. Print exactly one line. The line should contain exactly one real value which is the length of the shortest path between $S$ and $T$. Your output $z$ should be in the format that consists of its integer part, a decimal point, and its fractional part, and will be decided to be "correct" if it holds that $a - 10^{-3} < z < a + 10^{-3}$, where $a$ denotes the jury's answer. The Euclidean distance between two points $p = (x_1, y_1)$ and $q = (x_2, y_2)$ is $\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$.

12
0 5 2 8 5 3 7 6 11 4 13 0
11 8 3 3

10.077687

8
0 7 2 2 5 7 7 0
-2 4 6 4

11.767829

4
0 5 8 0
8 6 4 2

6.0