题目描述

Ladder game is a popular game in Korea, as well as China and Japan. Wikipedia says that “It is known in Korean as Sadaritagi (사다리타기, literally "ladder climbing"), in Japanese as Amidakuji (阿弥陀籤, "Amida lottery"), and in Chinese as Guijiaotu (鬼腳圖, literally "ghost leg diagram").”

The diagram where the game is played consists of $n$ vertical lines with horizontal line segments connecting two adjacent vertical lines. The horizontal line segments are called legs. Each vertical line has a starting (upper) point and an end (lower) point. The basic rule of this game is simple as follows:

• Start from the starting point of each vertical line and move downward along the vertical line. When encountering a leg, move along the leg to the adjacent vertical line, and continue downwards until reaching the end of a vertical line.

The vertical lines are numbered from 1 to $n$ from left to right. It is well known that the game result is a permutation of $[1,2,...,n]$. For example, given a diagram with 4 vertical lines and 5 legs shown below, the game result is $[2,3,4,1]$ from left to right.

:::align{center} :::

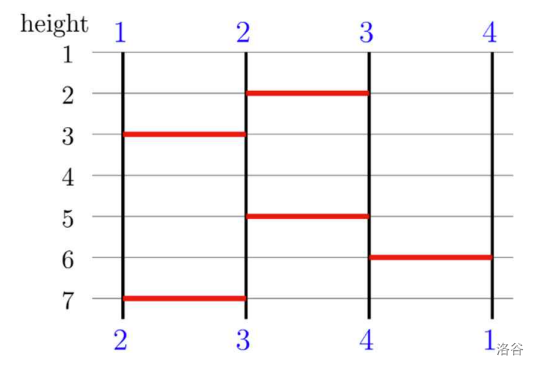However, some legs are redundant, meaning that the same result $[2,3,4,1]$ can be achieved with fewer legs; as in the figure below, one can obtain the same result only with three legs excluding topmost and bottommost ones. We want to determine the minimum number of horizontal line segments (legs) needed to achieve the same result. Note that it is possible to draw new legs than the given ones if necessary.

:::align{center} :::

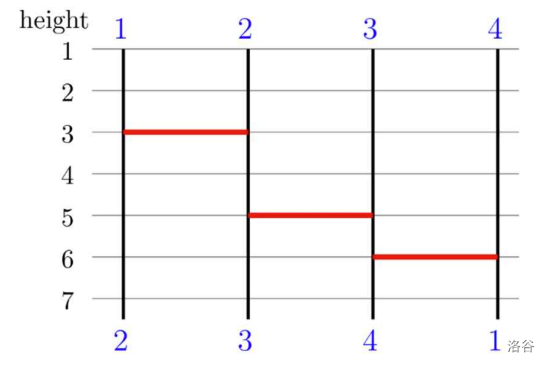You are given $q$ queries, where each query either adds a new leg or deletes an existing one. Write a program to output the minimum number of legs required to achieve the same game result of the ladder structure obtained after the query is processed. Note that each query is cumulative, meaning each subsequent query is applied to the ladder structure resulting from previous queries.

输入格式

Your program is to read from standard input. The input starts with a line containing three integers $n$, the number of vertical lines, $m$, the initial number of legs, and $q$, the number of queries, separated by a space where $2 \leq n \leq 100,000$, $1 \leq m \leq 100,000$, and $1 \leq q \leq 100,000$.

In the following $m$ lines, each line contains two positive integers $h$ and $a$, representing a leg at height $h$ connecting the $a$-th and $(a+1)$-th vertical lines ($1 \leq a \leq n-1$). The vertical lines are ordered from left to right, and the height is numbered from top to bottom starting with 1. The height is no more than $10^9$.

The next $q$ lines contain the query information. Each query is either in the form of $A\ h\ a$ or $D\ h\ a$, where $1 \leq h \leq 10^9$, $1 \leq a \leq n-1$.

• $A\ h\ a$: add a leg at height $h$ between the $a$-th and $(a+1)$-th vertical lines.
• $D\ h\ a$: delete the leg at height $h$ between the $a$-th and $(a+1)$-th vertical lines.

You can assume that there are no contradictory operations, that is, existing legs will not be added, and non-existing legs will not be deleted. Also, you can assume that no two legs are positioned such that they share the endpoint of the same height and the same vertical line.

输出格式

Your program is to write to standard output. The output consists of $q$ lines and each line contains the minimum number of legs required to achieve the same result for a query in the input order.

4 4 3
3 1
2 2
5 2
6 3
A 7 1
A 4 3
D 3 1

3
6
3

4 5 5
3 1
2 2
5 2
6 3
7 1
D 6 3
D 7 1
D 5 2
D 3 1
D 2 2

2
3
2
1
0

提示

Explanation for Sample Input 1:

The sample input 1 gives the initial ladder structure below. The game result is $[3,2,4,1]$.

:::align{center} :::

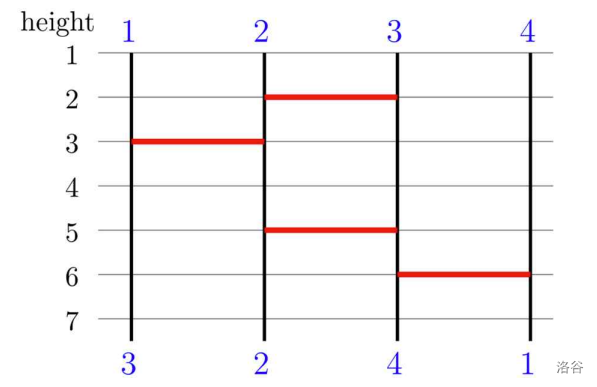After applying the first query $A\ 7\ 1$ in the figure blow, the ladder structure is changed, then the game result becomes $[2,3,4,1]$.

:::align{center} :::

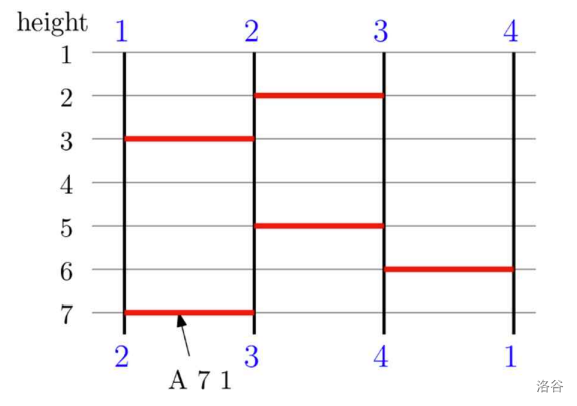Among the five legs, only three legs (without topmost and bottommost legs) are enough to achieve the same game result $[2,3,4,1]$ as shown in figure below, so the answer for the first query is 3.

:::align{center} :::

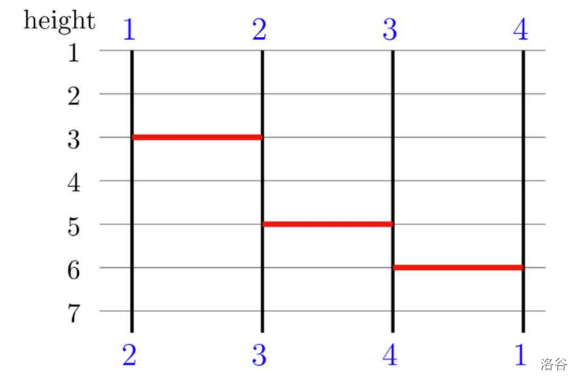After processing the second query $A\ 4\ 3$, the ladder structure is changed as shown below. The number of legs cannot be further reduced. The answer for the second query is 6.

:::align{center} :::

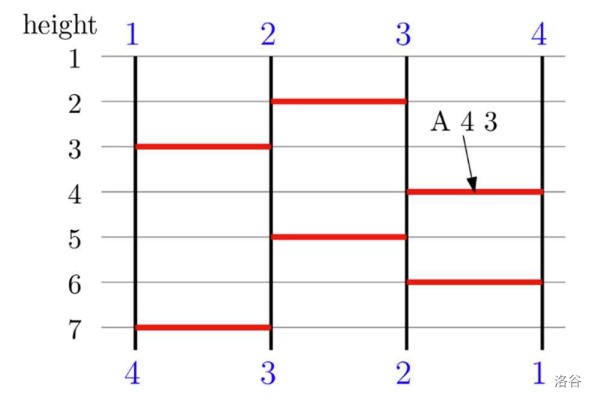After applying the third query $D\ 3\ 1$, the ladder structure is changed as shown below.

:::align{center} :::

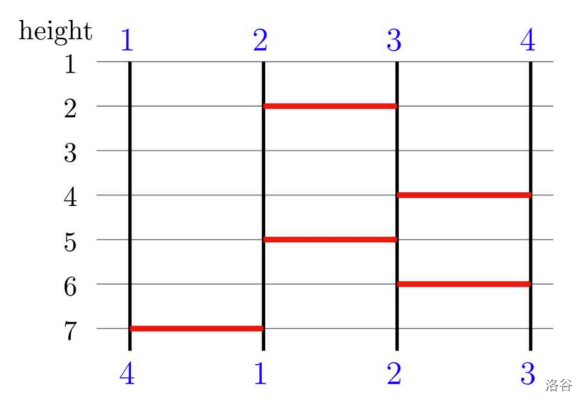The ladder structure with three legs as shown below guarantees the same game result, so the answer for the third query is 3.

:::align{center} :::
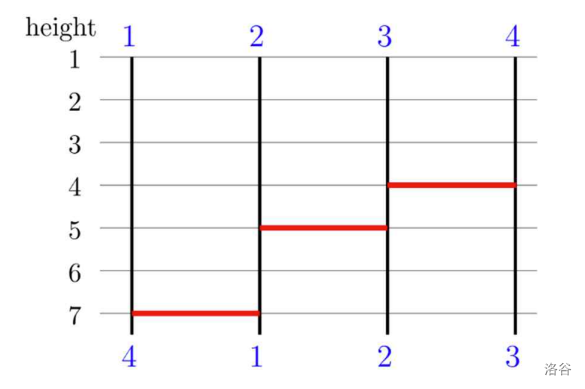