题目描述

The magician $B$ has $n$ cards in a row on a desk. Each card has two sides with colors. The top side of a card is the side facing upwards. The bottom side of a card is the side facing downwards. Each side of a card has one color. We want to find the maximum number of distinct colors on the top sides. In the following example, we are given 5 cards in a row on a desk. The colors of the top sides of the cards are violet, red, violet, violet, and red from the left to the right as shown in the following figure. The colors of the bottom sides of the cards are red, violet, blue, yellow, and red from the left to the right.

:::align{center} :::

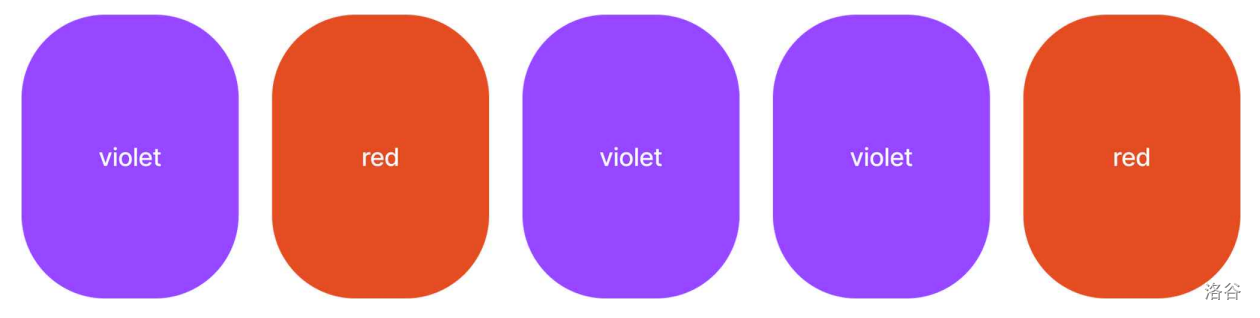If we flip a card, then the top side and the bottom side of the card are exchanged. If we flip the $3^{rd}$ and the $4^{th}$ card from the left, then the colors of the cards on the top sides become like the following.

:::align{center} :::

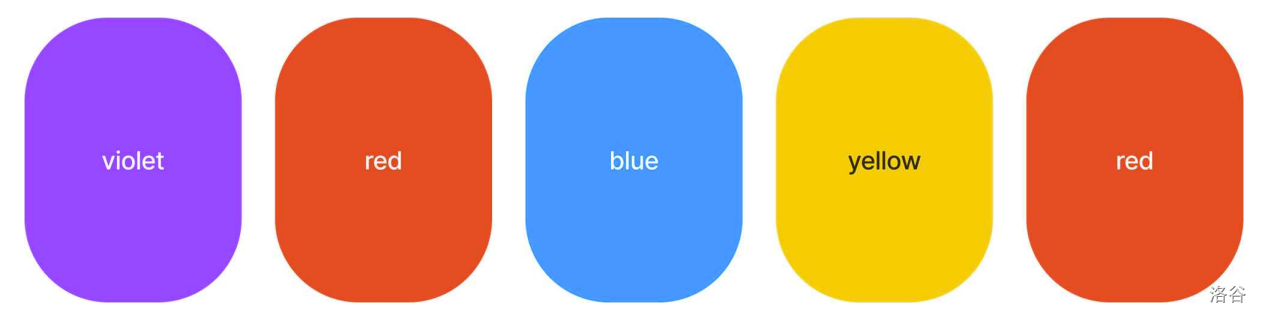The number of distinct colors on the top sides becomes $4$ which is the maximum for the example.

Given $n$ cards placed in a row on a desk and the colors on the sides of cards, write a program to output the maximum number of distinct colors on the top sides.

输入格式

Your program is to read from the standard input. The input starts with a line containing an integer $n$ ($1 \leq n \leq 200,000$), where $n$ is the number of cards. The cards are numbered from 1 to $n$. In the following two lines, the first line contains the colors on the top sides of cards from the card 1 to the card $n$. The second line contains the colors on the bottom sides of cards from the card 1 to the card $n$. Each color is represented by a nonnegative integer, not exceeding $10^6$.

输出格式

Your program is to write to the standard output. Print exactly one line. The line should contain the maximumnumber of distinct colors on the top sides.

5
0 1 0 0 1
1 0 2 3 1

4

2
3 5
5 1

2

3
0 1 0
1 0 2

3