题目背景

2025 年 9 月至 10 月期间，断断续续的雨笼罩了西安 30 余天。

Voidina 看着空中飘落的如烟小雨，开始了遐想。

题目描述

给定一颗无根树，共有 $n$ 个顶点。每个顶点 $i$ 都具有一个点权 $a_i$，初始所有点权都为 $0$。

你可以进行如下的操作最多不超过 $3n$ 次：

• 指定顶点的编号 $r,u\ (1 \le r,u \le n)$，使得这棵树暂时以顶点 $r$ 为根，随后对于顶点 $u$ 的子树中的每一个顶点 $v$，将其点权修改为 $a_v \oplus u$。此处的 $\oplus$ 表示按位异或。

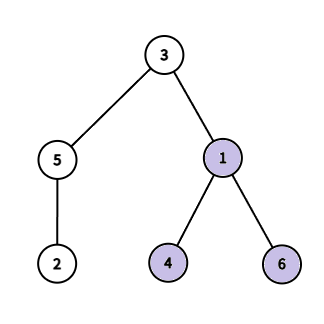
如图，当取 $r = 3$，$u = 1$ 进行操作时，顶点 $1,4,6$ 的点权会分别被异或上 $1$。

请你构造一个满足上述要求的操作序列，使得最终对于树中的每个顶点 $i$，都满足 $a_i = i$。

对于两个非负整数 $x,y$，它们的按位异或是指，将它们作为二进制数，对二进制表示中的每一位进行如下运算得到的结果：

• $x$ 和 $y$ 的这一位上不同时，结果的这一位为 $1$；
• $x$ 和 $y$ 的这一位上相同时，结果的这一位为 $0$。

比如，$10 \oplus 6 = (1010)_2 \oplus (0110)_2 = (1100)_2 = 12$。

输入格式

本题有多组数据。第一行一个正整数 $T\ (1\le T\le10^4)$，表示数据组数。

对于每组数据：

第一行一个整数 $n\ (1 \le n \le 2 \times 10^5)$，表示树的顶点数。

接下来 $n-1$ 行，每行两个整数 $u,v\ (1 \le u,v \le n,u \neq v)$，表示树中的一条边。

保证 $T$ 组数据中 $n$ 的和不超过 $2 \times 10^5$。

输出格式

对于每组数据：

第一行一个整数 $k$，代表你所构造的操作序列中操作的次数。

接下来 $k$ 行，每行两个整数 $r,u$，具体含义见题目描述。

1
2
1 2

2
1 2
2 1