题目描述

Mr. Kim is a stock market analyst. Recently, he found something interesting while looking at the stock charts of several companies. Most of the stocks that rose for four consecutive days fell the next day. Also, the stock price that fell on the fifth day was often located between the price of the second and third days of the stock price during the four days of the uptrend. For example, Company A's stock price was $500$ won, $560$ won, $600$ won, and $680$ won for four consecutive days, and the fifth day's stock price of Company A was $580$ won. Also, Company B's stock price was $1,000$ won, $1,200$ won, $1,400$ won, and $1,700$ won for four consecutive days, and the fifth day's stock price of Company B was $1,350$ won.

Mr. Kim thinks that if he can find a part in the previous stock price sequence that matches the price movement pattern over the last few days, he will be able to predict the stock price for the next day quite accurately. He also thinks that the relative ranks in a stock price sequence are more important than the actual prices because if the relative ranks of two stock price sequences are the same, their patterns in charts look similar. In the above example, the stock price sequence of Company A for five consecutive days, $500$ won, $560$ won, $600$ won, $680$ won, $580$ won, can be represented as $(1,2,4,5,3)$ because $500$ is the smallest among the five numbers, $550$ is the second smallest, $600$ is the fourth, and so on. Moreover, the stock price of Company B for five consecutive days, $1,000$ won, $1,200$ won, $1,400$ won, $1,700$ won, $1,350$ won, can also be represented as $(1,2,4,5,3)$ due to the same reason. Their relative ranks are the same and their charts of five consecutive days look very similar as shown in Figure K.1.

:::align{center}

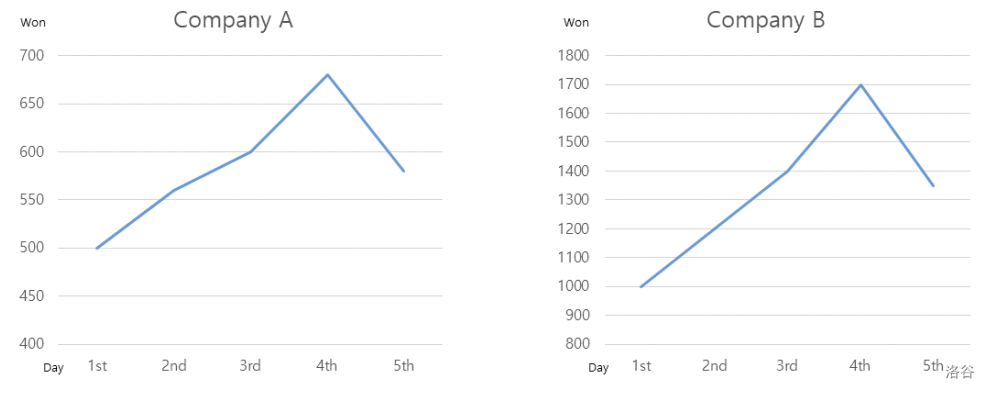
Figure K.1 Charts of Company A and B for five consecutive days :::

Mr. Kim decided to consider two sequences as a match if all the relative ranks of same positions of two sequences are the same. Mr. Kim formally defined R-match of two sequences of same length (number of integers) as follows: Two sequences of integers $x = (x_1, ..., x_m)$ and $y = (y_1, ..., y_m)$ of the same length are an R-match if and only if for each $i$ ($1 \le i \le m$), $x_i$'s rank in $x$ and $y_i$'s rank in $y$ are the same. Next, he defined the R-pattern matching problem as follows: Given two sequences of integers $x$ of length $m$ and $y$ of length $n$ ($m \le n$), find every position $i$ of $y$ such that $x$ and $(y_i, ..., y_{i+m-1})$ are an R-match. For example, when $x = (33,40,22,40,41,28)$, and $y = (10,20,16,27,32,12,32,33,20,25,15,25,31,17)$, $x$ and $(y_4, ..., y_9)$ are an R-match. Also, $x$ and $(y_9, ..., y_{14})$ are an R-match.

Given two sequences of integers $x$ of length $m$ and $y$ of length $n$ ($m \leq n$), write a program to solve the R-pattern matching problem for $x$ and $y$.

输入格式

Your program is to read from standard input. The input starts with a line containing two integers, $m$ and $n$ ($1 \leq m \leq 10,000$, $1 \leq n \leq 1,000,000$, $m \leq n$), where $m$ is the length of $x$, and $n$ is the length of $y$. In the second line, the $m$ integers in $x$ are given in turn. In the third line, the $n$ integers in $y$ are given in turn. Each integer in $x$ and $y$ ranges from $1$ to $10^9$.

输出格式

Your program is to write to standard output. Print exactly one line. The line should contain every position $i$ of $y$ such that $x$ and $(y_i, \dots, y_{i+m-1})$ are an R-match. Each position must appear in increasing order. If there is no such position, print $0$.

5 12
500 560 600 680 580
30 25 40 60 70 90 65 30 35 50 55 40

3 8

5 15
1000 1200 1400 1700 1350
1 2 3 4 5 6 7 8 7 6 5 4 3 2 1

0

6 14
33 40 22 40 41 28
10 20 16 27 32 12 32 33 20 25 15 25 31 17

4 9