题目描述

The management committee plans to introduce a new security system to monitor the museum at night time. The floor plane of the museum has a shape of a rectilinear polygon $P$ whose edges are either horizontal or vertical. In addition, $P$ has the $x$-monotone boundary, that is, the intersection of $P$ and any vertical line is either empty or a single line segment.

The new security system is based on infrared laser beam sensors. Moving along a straight track placed inside of $P$, an infrared laser beam sensor unit emits the laser beam in a direction perpendicular to the track. When it detects any motion, an emergency alarm is issued immediately.

Tracks are represented as horizontal or vertical line segments. Tracks are unlimited in length. A point $q$ in $P$ is monitored by a sensor located at a point $p$ on a track if $q = p$ or the following conditions are satisfied.

(i) The line segment connecting $p$ and $q$ does not meet the outside of $P$.

(ii) The track and the line segment connecting $p$ and $q$ are orthogonal to each other.

A polygon $P$ is said to be completely monitored by a set $T$ of tracks if each point inside $P$ is monitored by a sensor on a track of $T$. The committee wants to know the minimum number of infrared laser beam sensor units required to completely monitor the museum. There are two things to note. The first is that the boundary of $P$ do not intersect a track excluding its endpoints, and the second is that the tracks must not intersect each other, even at their endpoints. For example, at least 3 sensor units are required to monitor the $x$-monotone rectilinear polygon as shown in the figure below. In this figure, blue lines represent tracks.

:::align{center} :::

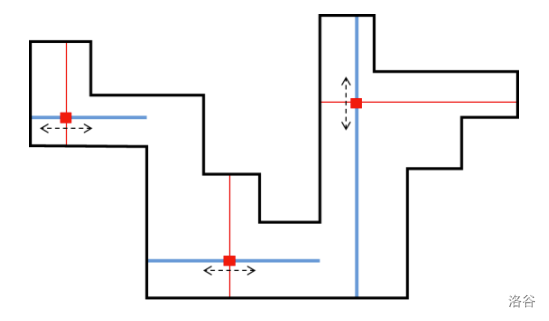Given an $x$-monotone rectilinear polygon, write a program to compute the minimum number of sensor units required to completely monitor the polygon.

输入格式

Your program is to read from standard input. The input starts with a line containing an integer, $n$ ($4 \leq n \leq 100,000$), where $n$ is the number of vertices of an $x$-monotone rectilinear simple polygon. The following $n$ lines give the coordinates of the vertices in counterclockwise direction. Each vertex is represented by two numbers separated by a single space, which are the $x$-coordinate and the $y$-coordinate of the vertex, respectively. Each coordinate is given as an integer between $-100,000,000$ and $100,000,000$, inclusively.

输出格式

Your program is to write to standard output. Print exactly one line. The line should contain an integer representing the minimum number of sensor units required to completely monitor the given polygon.

20
5 1
14 1
14 7
16 7
16 9
18 9
18 11
13 11
13 13
11 13
11 4
9 4
9 6
7 6
7 10
3 10
3 12
1 12
1 8
5 8

3

12
12 5
4 5
4 3
1 3
1 1
6 1
6 3
9 3
9 1
15 1
15 3
12 3

2