题目描述

There is a straight road on which two types trams run. One is an east-to-west tram which moves from east to west, and the other is a west-to-east tram. For each type, several trams run regularly, so anyone can ride the tram in any direction at any time. To use the tram, you have to pay a ticket for each direction you take. In other words, to use a tram that moves from east to west, you must pay a W-ticket (west bound ticket), and conversely, to use a tram that moves from west to east, you must pay an E-ticket (east bound ticket). You can get on and off the tram at any time and place you want, and once you get on the tram, you can ride it as long as you want.

Bob, a post office worker, goes to the post office every day to deliver the mails assigned to him. He uses the tram to deliver them. Each location where mail will be delivered is represented by an $x$-coordinate for convenience, and the post office locates at $x = 0$.

To deliver $n$ pieces of mail, the post office gives Bob $n$ tram tickets. Bob uses one ticket to deliver one piece of mail. However, among the $n$ tickets provided by the post office, the number of W-tickets is $w$ and that of E-tickets is $e$ ($e = n - w$). By using the tickets he received at the post office, Bob wants not only to figure out the order in which the $n$ pieces of mail should be delivered, but also to minimize the distance he travels using the tram.

Depending on the order in which the pieces of mail are delivered, it is divided into two types. The first type, denoted by $t = 1$, is the case that the order of mail delivery is not important. The second type, denoted by $t = 2$, is the case one specific designated piece of mail must be delivered at last and all the others can be delivered in any order.

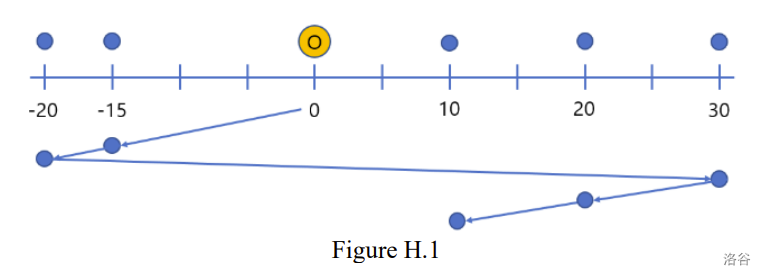
For example, suppose that $n = 5$, $w = 4$ (the number of W-tickets), $t = 2$, and the $x$-coordinates of the places where the mails should be delivered are $(-20, -15, 20, 30, 10)$, and that the $x$-coordinate of the specific designated mail which must be finally delivered is $x = 10$. The optimal delivery route is shown in Figure H.1 and the total distance moved using trams is 90. As shown in Figure H.1, four W-tickets and one E-ticket are used and the designated mail is delivered at last.

:::align{center} :::

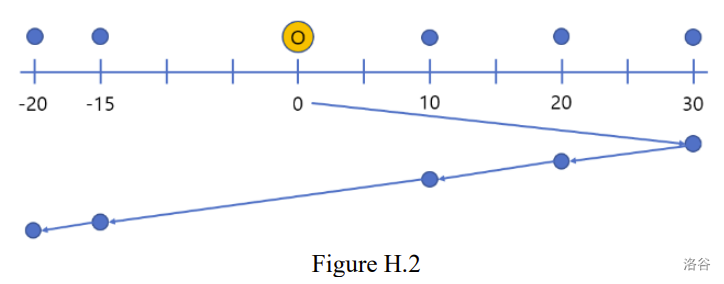
Consider another example where all information is the same as above except for $t = 1$. The optimal delivery route for this case is shown in Figure H.2 and the total distance is 80. In this case, you can see that four W-tickets and one E-ticket are used as well.

:::align{center} :::

Given information about the mail that Bob should deliver, write a program that finds the minimum distance he travels using trams.

输入格式

Your program is to read from standard input. The input starts with a line containing three integers, $n$, $w$ and $t$ ($1 \leq n \leq 3 \times 10^5$, $0 \leq w \leq n$, $1 \leq t \leq 2$), where $n$ is the number of pieces of mail, $w$ is the number of W-tickets, and $t$ indicates the delivery order type as explained above. Note that the number of E-tickets is $n - w$. In the following line, $n$ integers are given. The $i$-th integer $x_i$ ($1 \leq i \leq n$, $-10^9 \leq x_i \leq 10^9$, $x_i \neq 0$) is the $x$-coordinate of the location where the $i$-th mail should be delivered. When $t = 2$, $x_n$ denotes the $x$-coordinate of the specific designated mail that must be delivered at last.

You can assume no two $x_i$'s are the same.

输出格式

Your program is to write to standard output. Print exactly one line. The line should contain the minimum distance Bob travels to deliver all the pieces of mail. If it is impossible for Bob to deliver them using the tickets print $-1$.

5 4 2
-20 -15 20 30 10

90

5 4 1
-20 -15 20 30 10

80

7 1 2
10 13 -30 24 50 -5 -21

-1