题目描述

Given a collection of people who interact, we can define a graph whose vertices are people, with an edge between two people if and only if they are friends with one another. Such graphs are called social networks and are well defined on any set of people, for example, the students in a college or the residents of a small town. An entire science analyzing social networks has sprung up in recent years, because many interesting aspects of people and their behavior are best understood as properties of this friendship graph.

Given a friendship graph where the vertices are the students in the Problem Solving class, your job is to write a program that decomposes the students in the class into two groups, $A$ and $B$, so that the following three conditions are satisfied simultaneously:

• Each student in the class belongs to exactly one group, $A$ or $B$.
• Any two students in each group are friends with each other.
• The difference between the sizes of groups $A$ and $B$, denoted as $||A| - |B||$, is as small as possible.

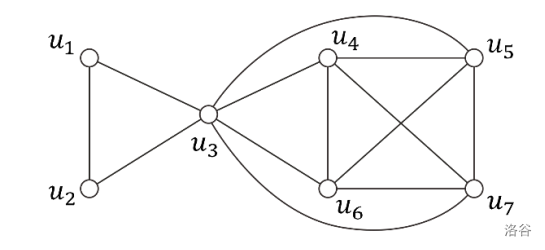
For example, suppose we are given a friendship graph shown in the figure below. Decomposing the students into $A = \{u_1, u_2, u_3, u_6\}$ and $B = \{u_4, u_5, u_7\}$ is not possible because $u_2$ and $u_6$ are not friends. On the other hand, in the decomposition into $A = \{u_1, u_2\}$ and $B = \{u_3, u_4, u_5, u_6, u_7\}$, any two students in each group are friends with each other; however, the size difference ($|2 - 5| = 3$) between the two groups is larger than the difference ($|3 - 4| = 1$) in the decomposition into $A = \{u_1, u_2, u_3\}$ and $B = \{u_4, u_5, u_6, u_7\}$. The last one is an optimal decomposition we want.

:::align{center} :::

输入格式

Your program is to read from standard input. The first line contains two integers $n$ and $m$, respectively indicating the numbers of vertices and edges of a friendship graph, in which we assume $2 \leq n \leq 1,000$ and $0 \leq m \leq \binom{n}{2}$. The vertices are indexed from $1$ to $n$. In the following $m$ lines, each line contains two integers $u$ and $v$ which represent an edge $(u, v)$ of the graph.

输出格式

Your program is to write to standard output. Print exactly one line that contains an integer. The integer should be the minimum of the size differences between two groups if the students can be decomposed into two groups satisfying the above three conditions; otherwise, the integer should be $-1$.

7 13
1 2
2 3
3 1
3 4
3 5
3 6
3 7
4 5
5 7
7 6
6 4
4 7
5 6

1

5 5
1 2
2 3
3 4
4 5
5 1

-1

4 4
4 3
3 2
2 1
1 4

0