题目描述

A rooted ordered tree $T$ can be expressed as a string of matched parentheses $p(T)$. The string representation $p(T)$ can be defined recursively. As a base case, a tree consisting of a single node is expressed by a pair of parentheses $()$. When a rooted ordered tree $T$ consists of a root node and $k$ ordered subtrees $T_1, T_2, ..., T_k$ having their roots as child nodes of the root node, the string representation $p(T)$ is defined as follows:

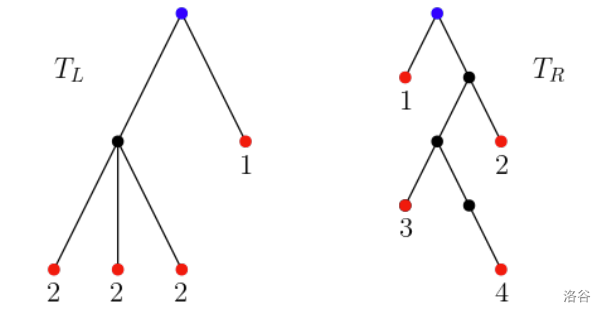
In the above expression, the operator $+$ means the concatenation of two strings. The figure below shows two examples of rooted ordered trees. The string representations $p(T_L)$ and $p(T_R)$ are $((())()())$ and $(()((()(()))()))$, respectively.

:::align{center} :::

The distance from the root node to a leaf node is defined as the number of edges to be traversed to reach the leaf from the root. In the figure above, the root nodes are colored in blue, and the distances from the root node to all leaf nodes are shown. For trees $T_L$ and $T_R$, the sum of the distances from the root to all leaf nodes are 7 and 10, respectively.

Given a string of matched parentheses representing only one rooted ordered tree, write a program to output the sum of the distances from the root of the tree to all leaf nodes.

输入格式

Your program is to read from standard input. The input consists of one line containing a string of matched parentheses which represents only one rooted ordered tree. The input does not contain any characters other than parentheses, and the length of string is at least 2 and no more than $10^7$.

输出格式

Your program is to write to standard output. Print exactly one line. The line should contain the sum of the distances from the root of the rooted ordered tree to all leaf nodes.

((()()())())

7

(()((()(()))()))

10