题目描述

A GPS navigation company ICPC (International Control Perfection Company) designs a car navigation system for a transportation network. The system abstracts the transportation network as a directed graph $G(V, E)$ with edge cost $c$. For a directed edge $(v, w) \in E$, $c(v, w)$ denotes the distance from a place $v \in V$ to another place $w \in V$. The company wants to implement the shortest path module in the system. To reflect the normal situation that we cannot turn to some directions in a junction of transportation network, we want to find the shortest path that does not contain forbidden turns as a subpath.

A path from $v$ to $w$ is a sequence of vertices $(v_1, v_2, \cdots, v_k)$ where $v_1 = v$, $v_k = w$, $(v_i, v_{i+1}) \in E$ for $1 \leq i \leq k-1$. Unlike the common definition of the path, you are here allowed to repeat the same vertices in a path one or more. A subpath of a path is a contiguous subsequence of the sequence that corresponds to the path. A forbidden turn is a path (i.e., triplet) $(x, y, z)$ such that $x, y, z \in V$ and $(x, y) \in E$ and $(y, z) \in E$. The distance of a path $(v_1, v_2, \cdots, v_k)$ is defined as $\sum_{i=1}^{k-1} c(v_i, v_{i+1})$. The shortest path from $v \in V$ to $w \in V$ is a path from $v$ to $w$ with the minimum distance. The company wants to find the distance of the shortest path that avoids the forbidden turns between two designated vertices. Note that the shortest path from $v \in V$ to $v \in V$ has distance 0 and it avoids all the forbidden turns.

Let's see the following example in the figure below. Each edge cost lies beside each edge and the list of three forbidden turns are in the right box. The shortest path without forbidden turns from the vertex 3 to the vertex 2 is $(3, 0, 1, 5, 4, 1, 2)$ which is denoted as blue arrows in the following figure. The distance of the shortest path is $3 + 12 + 4 + 7 + 8 + 2 = 36$. Note that we cannot take the shorter paths $(3, 0, 1, 2)$ and $(3, 0, 1, 5, 2)$ since they contain forbidden turns $(0, 1, 2)$ and $(1, 5, 2)$, respectively.

:::align{center} :::

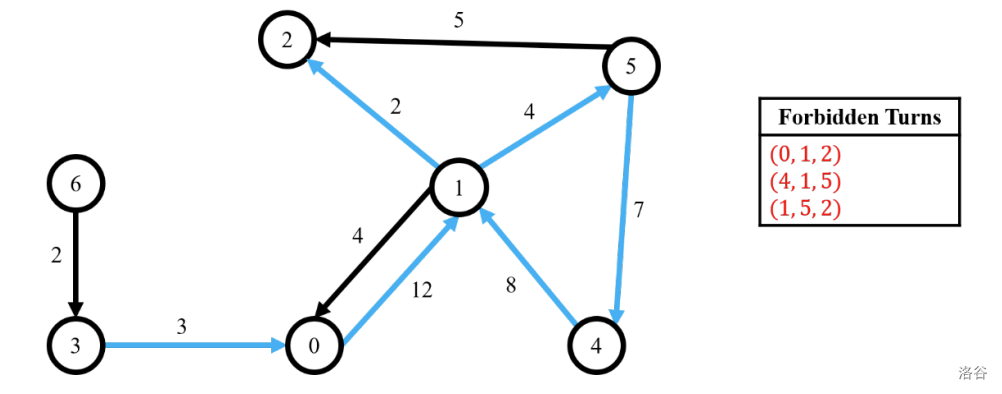Given a directed graph $G(V, E)$ with the edge cost $c$, a set of forbidden turns $F$, and two vertices $v$ and $w$, write a program to output the distance of the shortest path from $v$ to $w$ that avoids all the forbidden turns. We assume that out-degree of each vertex $v$, i.e., the number of edges that starts from $v$ is at most 10.

输入格式

Your program is to read from standard input. The input starts with a line containing three integers, $m$, $n$, and $k$. ($0 \leq m \leq 10n$, $1 \leq n \leq 30,000$, $0 \leq k \leq 500,000$), where $m$ is the number of directed edges, $n$ is the number of vertices, and $k$ is the number of forbidden turns of the given directed graph $G(V, E)$. Here, $k$ is less than or equal to the number of all the possible forbidden turns in the given directed graph $G(V, E)$. The vertices are numbered from 0 to $n-1$. The second line contains two integers $v$ and $w$ which denote the source and destination vertices, respectively. In the following $m$ lines, the $i$-th line contains three integers $x_i$, $y_i$, and $c_i$ ($0 \leq x_i \ne y_i \leq n-1$ and $0 \leq c_i \leq 10^3$) which denotes an edge $(x_i, y_i) \in E$ and its cost, respectively. In the following $k$ lines, the $i$-th line contains three integers $x_i$, $y_i$, and $z_i$ which denote a forbidden turn $(x_i, y_i, z_i)$.

输出格式

Your program is to write to standard output. Print exactly one line. The line should contain an integer that represents the distance of the shortest path from $v$ to $w$ which avoids all the forbidden turns. If such a path does not exist, the line should contain $-1$.

9 7 3
3 2
6 3 2
3 0 3
0 1 12
1 0 4
1 2 2
1 5 4
4 1 8
5 4 7
5 2 5
0 1 2
4 1 5
1 5 2

36

4 4 1
0 3
0 1 2
1 2 3
0 2 7
2 3 10
0 1 2

17

4 4 0
0 3
0 1 2
1 2 3
0 2 7
2 3 10

15