题目描述

There is a folding stick made up of $n$ segments of positive length. The segments are connected by hinges (stretchable strings), allowing the segments to be folded 180 degrees at each hinge. The wrapping length is said to be the length of the folded stick after the stick is folded at hinges one or more. Depending on the folding strategy, the wrapping length may be different.

You are to find the minimum wrapping length under the condition that the stick is folded in the following way: First, place the segments of the stick along a horizontal line. Then, fold the stick clockwise from left to right. During folding, the segment attached to the left side of each hinge rotates 180 degrees clockwise or not at all.

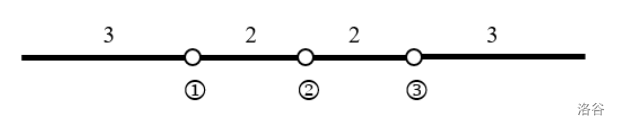
For example, the figure below shows a four-segment stick with a sum of segment lengths of 10. In the figure, the lengths of the segments are 3, 2, 2, and 3 from left to right, and the hinges are marked with ①, ②, ③.

:::align{center} :::

In this example, the stick cannot be folded at both hinges ① and ②. This is because if the stick is folded at hinge ① and then at hinge ②, the segment with length 3 passing over the hinge ② will be broken. If it is folded only at hinge ②, the wrapping length is 5. If it is folded at hinges ① and ③ in order, the wrapping length is 4 as shown in the figure below.

:::align{center} :::

Given a sequence of segments lengths of a folding stick, write a program to output the minimum wrapping length of the stick.

输入格式

Your program is to read from standard input. The input starts with a line containing an integer, $n$ ($2 \leq n \leq 100,000$), where $n$ is the number of segments of a folding stick. The next line contains $n$ positive integers which represent a sequence of lengths of segments from the leftmost one to rightmost one of the stick. Each segment length is no more than 20,000.

输出格式

Your program is to write to standard output. Print exactly one line. The line should contain the positive integer representing the minimum wrapping length.

4
3 2 2 3

4

5
1 1 1 1 1

1

7
1 3 2 3 4 2 2

6