题目描述

A quadrilateral is a polygon with exactly four distinct corners and four distinct sides, without any crossing between its sides. In this problem, you are given a set $P$ of $n$ points in the plane, no three of which are collinear, and asked to count the number of all quadrilaterals whose corners are members of the set $P$ and whose interior contains no other points in $P$.

:::align{center} :::

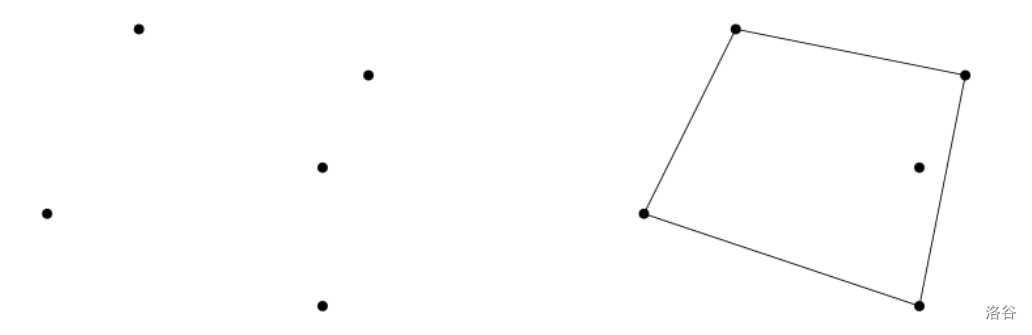
For example, assume that $P$ consists of five points as shown in the left of the figure above. There are nine distinct quadrilaterals in total whose corners are members of $P$, while only one of them contains a point of $P$ in its interior, as in the right of the figure above. Therefore, there are exactly eight quadrilaterals satisfying the condition and your program must print out 8 as the correct answer.

输入格式

Your program is to read from standard input. The input starts with a line containing an integer $n$ ($1 \leq n \leq 300$), where $n$ denotes the number of points in the set $P$. In the following $n$ lines, each line consists of two integers, ranging from $-10^9$ to $10^9$, representing the coordinates of a point in $P$. There are no three points in $P$ that are collinear.

输出格式

Your program is to write to standard output. Print exactly one line consisting of a single integer that represents the number of quadrilaterals whose corners are members of the set $P$ and whose interior contains no other points in $P$.

5
0 0
2 4
6 2
6 -2
7 3

8

4
0 0
10 0
5 10
3 2

3

10
10 10
1 0
4 8
-1 -4
-7 -4
-3 2
5 -10
-10 -5
1 1
5 -3

170