题目描述

The ICPC kingdom has decided to build a new castle. The boundary of the castle is designed as a rectilinear polygon with edges parallel to the $x$-axis or to the $y$-axis. To minimize the damage exposed by the enemy attack, the kingdom wants to minimize the perimeter of the rectilinear polygon. Let us go into more detail.

A rectilinear polygon $P$ of $n$ vertices with integer coordinates realizes a turn sequence $S$ of length $n$ of two letters L and R if there is a counterclockwise traverse along the boundary of $P$ such that the turns at vertices of $P$, encountered during the traverse, form the turn sequence $S$; the left turn at a convex vertex corresponds to L and the right turn at a reflex vertex corresponds to R. For example, the rectilinear polygon in Figure B.1(a) realizes the turn sequence $S = \text{RLLRLLLLRRLRIRLLL}$ of length 16. Another turn sequence $S = \text{LLRLLRLLRLLRLLR}$ of length 14 can be realized by rectilinear polygons in Figure B.1(b) and B.1(c). Note that a turn sequence can have infinitely many realizations of rectilinear polygons in the integral plane.

A polygon is simple if there are no two edges that intersect except at the end vertices of adjacent edges. A polygon is monotone to an axis if its intersection with a line orthogonal to the axis is at most one segment. The monotone polygon is called 2-monotone if it is monotone to both $x$-axis and the $y$-axis, and 1-monotone if it is monotone to the one axis but not to the other axis. For example, the polygon in Figure B.1(a) is 1-monotone because it is monotone to only one axis, the $x$-axis, while the polygons in Figure B.1(b) and B.1(c) are 2-monotone. A turn sequence is also said to be $t$-monotone if any simple rectilinear polygon realizing the turn sequence is $t$-monotone where $t = 1, 2$.

:::align{center}

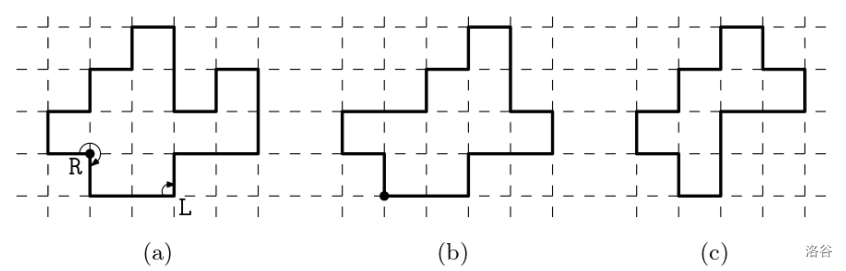
Figure B.1 (a) A simple 1-monotone rectilinear polygon realizing a 1-monotone turn sequence RLLRLLLRRLLRIRLLL (starting from the marked vertex). (b) A simple 2-monotone rectilinear polygon realizing a 2-monotone turn sequence LLRLLRLLRLLRLLR (starting from the marked vertex). (c) The 2-monotone rectilinear polygon with the minimum perimeter for the turn sequence in (b). :::

The perimeter of a rectilinear polygon is the sum of the length of its edges. The perimeter of the polygon in Figure B.1(b) is 18, but this is not minimum for LLRLLRLLRLLRLLR. Its minimum perimeter should be 16 as in Figure B.1(c).

Given a $t$-monotone turn sequence of $n$ turns for $t = 1, 2$, write a program to compute the minimum perimeter of simple $t$-monotone rectilinear polygons that realize the input $t$-monotone turn sequence.

输入格式

Your program is to read from standard input. The input is one line containing a string of $n$ turns of two uppercase letters L and R that is a $t$-monotone turn sequence, where $t = 1, 2$ and $4 \leq n \leq 10^{t+3}$.

输出格式

Your program is to write to standard output. Print exactly one line. The line should contain the positive integer that is the minimum perimeter of simple $t$-monotone rectilinear polygons that realize the input $t$-monotone turn sequence for $t = 1, 2$.

LLRLLRLLRLRLLR

16

RLLRLLLRRLLRLRLL

20

LLRRLLLLRRLL

16

RLLRLLRLLRLL

12